Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » obsah rovinného obrazce (TOTO TÉMA JE VYŘEŠENÉ)
#2 01. 07. 2008 09:00
Re: obsah rovinného obrazce
Jestliže si ten parametrický zápis převedu do normálního (za t dosadím +-odmocninu z x/3), vyjde funkce ve tvaru  . Grafem je křivka, která protíná osu x v nule a ve trojce. (viz obr.,doufám že je to dobře)
. Grafem je křivka, která protíná osu x v nule a ve trojce. (viz obr.,doufám že je to dobře)
100*0>0 aneb stokrát nic umořilo osla
Offline
#5 01. 07. 2008 10:03
Re: obsah rovinného obrazce
thriller: bohužel je to špatně, ty jsi kreslil graf funkce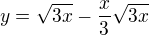
Skutečný průsečík je pro x = 9, tj. pro 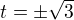
Pak integrujeme od 0 do 9 a vynásobíme dvěma.
Offline
#6 01. 07. 2008 11:00
Re: obsah rovinného obrazce
je-li funkce zadaná parametricky - rovnicemi x=x(t) a y=y(t), t je z <a,b> a platí, že tvoří uzavřenou plochu (graf se protíná právě v bodech parametru a,b) - vypočítáme obsah této plochy následovně 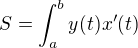
ale to přeci platí i když funkci zinvertujem, ale s opačným znaménkem, takže zárověň 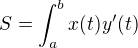
z toho dostávámé 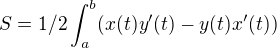
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » obsah rovinného obrazce (TOTO TÉMA JE VYŘEŠENÉ)

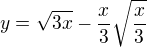 , vyjde plocha vrchní poloviny toho "bobanu" a pak bych to vynásobil dvěma.
, vyjde plocha vrchní poloviny toho "bobanu" a pak bych to vynásobil dvěma.