Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 12. 10. 2011 16:34
5 boký pravidelný jehlan
Výška pravidelného pětibokého jehlanu je stejně dlouhá jako hrana podstavy, a to 20 cm. Vypočtěte objem a povrch.
Objem mám vypočten Podstavu taky ale nevím jak na Plášť protože nevím jak vypočíst stěnovou výšku pry se to počítá nějak přes hustota/a?
Děkuji za rady
Offline
- (téma jako vyřešené označil(a) frank_horrigan)
#2 12. 10. 2011 16:54 — Editoval frank_horrigan (12. 10. 2011 16:57)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: 5 boký pravidelný jehlan
přes hustotu??? koho to napadlo? btw, hustotu čeho?
když si to rozkreslíš, tak uvidíš: výšku, to je jedna odvěsna. Poloměr vepsaný kružnice (pokud hledáš stěnovou výšku) si zjistíš, na to máš vzoreček. To ti poslouží jako druhá odvěsna. Vypočítej přeponu, což bude stěnová výška.
Nebo taky to můžeš počítat přes stranu, pak zjišťuješ poloměr opsané kružnice, který ti poslouží jako odvěsna
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#4 12. 10. 2011 17:50 — Editoval frank_horrigan (12. 10. 2011 17:56)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: 5 boký pravidelný jehlan
ok,
zkusme to přes tu vepsanou kružnici. Znáš-li hranu (tedy stranu toho pětiúhelníku), pak platí vzorec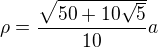 , kde
, kde  je strana pětiúhelníka (neboli hrana podstavy). Už dosadíš?
je strana pětiúhelníka (neboli hrana podstavy). Už dosadíš?
A až to budeš mít, tak mi prosím řekni, co máš s tou hustotou?? Jediné, co mně napadá, že hustota se značí  , a poloměr vepsané kružnice také tak...
, a poloměr vepsané kružnice také tak...
Ale, pomůže-li to, a nebude-li tě to tolik mást, tak si poloměr vepsané kružnice označ třeba 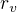 , jak chceš
, jak chceš
EDIT: až vypočteš ten poloměr ( nebo
nebo 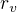 , je mi jedno jak si to označíš, jen tomu prosím neříkej hustota, hustota je fyzikální veličina (no, to délka nakonec taky), která se od délky velmi, ale velmi liší :)
, je mi jedno jak si to označíš, jen tomu prosím neříkej hustota, hustota je fyzikální veličina (no, to délka nakonec taky), která se od délky velmi, ale velmi liší :)
takže až vypočteš ten poloměr, tak uvidíš pravoúhlý trojúhelník, kde jedna odvěsna je ten poloměr, druhá odvěsna je výška jehlanu, a stěnovou výšku už si dopočítáš (pythagora doufám znáš a dokážeš do něj dosadit :) )
EDIT2: ten vzorec pro ty poloměry bys měl/a najít v matematických tabulkách, samozřemě jde i odvodit, ale to není práce na chvilku, takže buď vyhledat, nebo si ho hold pamatovat
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
#6 12. 10. 2011 17:58 — Editoval frank_horrigan (12. 10. 2011 17:58)
- frank_horrigan


- Příspěvky: 938
- Reputace: 31
Re: 5 boký pravidelný jehlan
Promiň, moje blbost... použij jsem vzorec pro opsanou, nikoli vepsanou...
Tak, tady je nový vzorec (správný):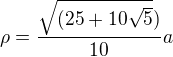
The only thing worse than being wrong is staying wrong
Sun Tzu - The Art of War
Offline
