Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 08. 11. 2007 23:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prusečíky s osou x
Prusecik s osou x je bod, ktery ma souradnice (x, 0) proto dosadime za y = 0
0=(12x^3-5x^2-6x-1)/(4x+1)
(12x^3-5x^2-6x-1) = 0 a zároven (4x+1) nesmí byt 0.
je to polynom 3 stupne, jeden koren odhadneme, je to x = 1, polynom rozlozime:
(x-1).(12x^2 + 7x +1) a najdeme dalsi koreny (resime kvadratickou rovnici v zavorce).
Celkem najdeme 3 reseni, zkontrolujeme, zda zadne neodporuje podmince.
Je to tak dost podrobne? Jinak se ozvi, bude dovysvetleno
Offline
#4 09. 11. 2007 11:25
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prusečíky s osou x
Umis derivovat? pokud ano, tak derivuj, pokud ne, tak vrchol bude mit x-souradnici uprostred usecky mezi dvou pruseciku, musich pak ale overit, zda je to vrchol (lokalni max) nebo naopak "hloubka" (lokalni min). souradnice pruseciku serad za sebou a vypocti x - souradnici stredu usecky.
Offline
#7 09. 11. 2007 17:43
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prusečíky s osou x
Pro Almion:
http://mathonline.fme.vutbr.cz/download … d_file=747 Hornerovo schema
Offline
#8 09. 11. 2007 19:06
Re: Prusečíky s osou x
jelena mela dobrou vuli odpovedet Almionovi, ale Hornerovo schema neni metodou pro vypocet obecneho korene kubicke rovnice, nebo chcete-li rozklad kubickeho mnohoclene na linearni faktory. Pouzil bych Cardanovy vzorce (to je to celkem neprijemna a kompikovana zalezitost, ale marna slava) nebo nejake jine metody.
Offline
#9 09. 11. 2007 19:17
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prusečíky s osou x
Pro Mariana:
Srdecne zdravim, moje poznamka nebyla ani tak ke kubicke rovnici konkretne, mela jsem na mysli obecne rozklad mnohoclenu (tak jsem rozumela otazce) - tam se prece Hornerovo schema vyuziva nebo se mylim?
Offline
#10 09. 11. 2007 19:37 — Editoval Marian (09. 11. 2007 19:39)
Re: Prusečíky s osou x
No nevim, jestli by se to dalo aplikovat. Uvedu polynom ![kopírovat do textarea $p(x)\in\mathbb{Z}[x]$](/mathtex/cb/cb0f2d2f2b73f5e984baf870528162a4.gif) , ale nevim, jak bych jej "rozkladal" (nad telesem C, at ma smysl hovorit o obecnych polynomech a existenci rozkladu). Tedy necht
, ale nevim, jak bych jej "rozkladal" (nad telesem C, at ma smysl hovorit o obecnych polynomech a existenci rozkladu). Tedy necht  ,
,
kde 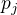 znaci j-te prvocislo. Nevim, jak bych pouzil Hornerova schematu k nalezeni rozkladu tohoto polynomu. Ale vybral jsem pripad prilis komplikovany. Snadno bych zkonstruoval jiny (jednodussi) polynom, ktery nerozlozim pomoci Hornerova schematu.
znaci j-te prvocislo. Nevim, jak bych pouzil Hornerova schematu k nalezeni rozkladu tohoto polynomu. Ale vybral jsem pripad prilis komplikovany. Snadno bych zkonstruoval jiny (jednodussi) polynom, ktery nerozlozim pomoci Hornerova schematu.
Dle meho nazoru Hornerovo schema primarne slouzi k nalezeni funkcni hodoty polynomu v zadanem bode  . Nekdy se pak da jiste pouzit k nalezeni rozkladu, ale je to loterie. Nejprve onoho potencialniho kandidata na koren musim nejak najit, a pote Horner odpovi, jak se tento kandidat "hodi" na pozici nuloveho bodu. Navic rovnice pateho radu jiz nejdou resitelne pomoci radikalu a neni znam obecny algoritmus pro nalezeni nulovych bodu takovychto polynomu.
. Nekdy se pak da jiste pouzit k nalezeni rozkladu, ale je to loterie. Nejprve onoho potencialniho kandidata na koren musim nejak najit, a pote Horner odpovi, jak se tento kandidat "hodi" na pozici nuloveho bodu. Navic rovnice pateho radu jiz nejdou resitelne pomoci radikalu a neni znam obecny algoritmus pro nalezeni nulovych bodu takovychto polynomu.
Nevidim tedy v tomo pripade duvod, proc by v "obecnem" pripade mohl slouzit prostredek zvany Hornerovo schema k nalezeni nulovych bodu nebo rozkladu polynomu, kdyz k tomuto ucelu ani neslouzi v podstatne jednodussich pripadech.
Offline
#11 10. 11. 2007 01:37 — Editoval jelena (10. 11. 2007 01:37)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prusečíky s osou x
Mariane, navrhuji poprosit kolegu Almiona o doplneni, zda se ptal na reseni kubicke rovnice - souhlasim, neni to jednoducha zalezitost, mas pravdu ohledne Cardanovych vzorců apod., ale pokud se ptal na rozklad polynomu, mam za to, ze prave Hornerovo schema je vyucovano na strednich skolach a na VS technickych jako postup pro rozklad polynomu za predpokladu, ze koren je cele cislo. Alespon nevim, ze by nejak podrobne vyucovalo neco jineho, pak neco jineho se vyucuje az v numerickych metodach. To jen tak na doplneni, proc jsem zareagovala prave Hornerem :-)
Offline
#12 10. 11. 2007 13:53
Re: Prusečíky s osou x
Zdravim, jeleno!
Hned od zacatku jsem vedel, o co ti jde. Tusil jsem, ze smerujes k celociselnym kandidatum na nulove body. Nechal jsem te trochu topit se v mych reakcich, ale zle jsem to vubec nemyslel. Prave naopak.
Stale musim ale trvat na tom, ze to neni (efektivni) metoda pro urcovani korenu by? jednoduchych polynomickych rovnic. Tezko budu hledat nulovy bod v oboru celych cisel, neexistuje-li takovy. Zde tudiz tato technika (Horn. sch.) selze. Existuji nektera kriteria, ktera nam davaji jednoznacnou odpoved na to, zda-li celociselny koren, nebo take racionalni koren, polynomicke rovnice s celociselnymi koeficienty existuje. Jedno z nich ma dokonce specialni nazev, totiz Eisensteinovo kriterium. Jina asi nejak specialne pojmenovana nejsou. Mam li tudiz kandidata na nulovy bod (ale nejprve jej musim najit), pak Hornera beru, ale jinak nikoliv. Slo mi o to, ze jsi, mimo jinych -- tedy me a Almiona, pouzila slovo "obecne". V obecnem pripade se celociselny koren muze nachazet na ciselne ose x libovolne vzdalene od pocatku soustavy souradnic. Tudiz nemusi byt zrovna lehke nalezt takoveto celociselne reseni, natoz pomoci Hornerova schematu.
Ale existuji samozrejme specialni vzorce (odhady), ktere nam udavaji, v jakem intervalu se nachazeji vsechny nulove body polynomickych funkci. Jiste si na ne vzpomenes. Jsou zavisle na koeficientech polynomicke rovnice. Pokud nalezneme takovyto odhad, a neni to tezke, pak bych se snad priklonil k tomu, ze Hornerovo schema je pouzitelne. Ale i zde v "obecnem" pripade muze tento interva byt libovolne velky.
Priklanim se ale k tomu, ze na technickych VS, popr. na SS je Horner relativne efektivni metodou. O obecnem pripade vsak nelze diskutovat. To vsak jiste chapes. Predpokladam, ze jsi studovala matematiku na nejake prirodovedecke fakulte, takze znas problematiku "obecneho" reseni polynomickych rovnic.
Prijemny den preje Marian!
Offline
#13 11. 11. 2007 21:04
Re: Prusečíky s osou x
Mnohokrat diky za odpovedi... Co se me tyce, chtel jsem predevsim vedet, jak zjistim koreny kubicke rovnice, protoze jsem nabyl dojmu, ze bych postup mel par mesicu pred maturitou znat... Bohuzel mam pocit, ze vetsinu z toho, o cem mluvite, vidim poprve v zivote, takze mi chvili potrva, nez si vse poradne proctu a zjistim, jak to tedy vubec resit a jestli sem otazku nemohl polozit lepe....
Offline
#14 14. 11. 2007 00:39 — Editoval jelena (14. 11. 2007 21:59)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Prusečíky s osou x
Pro Almiona
-ujistuji, ze v maturitnich otazkach reseni kubicke rovnice v obecnem smyslu nebude, pokud si vzpominam, je tam vyuziti pri reseni rovnic rozkladu mnohoclenu na soucin (ten mnohoclen bude urcite rozlozitelny), Horner se bere v seminari.
V kazdem pripade hodne zdaru pri priprave k maturite
Pro Mariana
:-) nechat nekoho topit, no toto, doufam, ze jsi mel pripraveno alespon zachranne lano, rozhodne ale to slovo "topit" vyvolalo jednu asociaci a tak posilam specialni pozdrav, kvalita je velmi skromna, ale nenasla jsem lepsi (snad bude fungovat :-) http://bards.pp.ru/IVC/AlmaMater/13_Pog … fregat.mp3 i s obrazkem :-)http://www.tmn.fio.ru/works/84x/306/57.htm
Studovala jsem skolu technickou, a to VS specialni chemicke technologie, pozadavky na znalosti matematiky byly docela tvrde, ale spise v praktickem pouziti. Proto se nerada poustim do teoretickych debat, ale opravdu jsem vdecna za tvuj cas, ktery venujes teoretickym zakladum jednotlivych rozebiranych prikladu a temat. Dekuji a zdravim.
Offline
