Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 11. 10. 2011 19:41
Definiční obory funkcí
Dobrý večer, dostali jsme úkol s určením def. oborů funkcí. Problém je, že jsem to nějak pozapoměl a nemůžu se hnout. Prosím proto o radu :) Děkuji.
P.S.: Vím, že se to musí umocnit. Ale neumím udělat začátek. Resp. jestli to převést jednu abs. hodnotu na jednu stranu umocnic. A pak nevím, přesně jak to umocnit. Není mi to moc jasný, nedělal jsem to dlouho a zapoměl jsem to. Děkuji
Offline
- (téma jako vyřešené označil(a) janca361)
#2 11. 10. 2011 19:45 — Editoval mikl3 (11. 10. 2011 19:46)
Re: Definiční obory funkcí
↑ tesarin: neumocňoval bych, protože tím se ztratí jedna podmínka a to sice, že odmocňovat umíme jen čísla větší nebo rovna nule (pokud se nebavíme o komplexních číslech), kdybys to navíc umocnil, co bys dostal na straně levé? předpis funkce na druhou?
jsou tam absolutní hodnoty, z toho vyplývají nulové body, které určí intervaly a v těch intervalech zkoumej, jak vypadá funkce
Offline
#4 13. 10. 2011 17:14 — Editoval Wotton (13. 10. 2011 17:14)
Re: Definiční obory funkcí
↑ tesarin:
ano, to je špatně, zkus si třeba dosadit za x dvojku.
Udělej to jak psal ↑ mikl3:. Najdi nulové body. Tím získáš tři různé funkce pro tři různé intervaly a vyšetřuj každou zvlášť (samozřejmě pouze na daném intervalu)
Dva jsou tisíckrát jeden.
Offline
#6 13. 10. 2011 17:48 — Editoval ((:-)) (13. 10. 2011 18:04)
Re: Definiční obory funkcí
↑ tesarin:
Nulové body: pre prvú absolútnu hodnotu  pre druhú absolútnu hodnotu
pre druhú absolútnu hodnotu 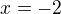 .
.
Položíš výraz v absolútnej hodnote rovný 0. Zistíš tak hranice, v ktorých sa mení znamienko výrazu v absolútnej hodnote.
Tieto body rozdelia číselnú os na 3 časti, v každej je znamienko výrazov v absolútnej hodnote nejaké a podľa toho vyzerá aj tvar riešenej nerovnice.
Absolútna hodnota je pre kladné hodnoty to isté číslo (výraz), pre záporné hodnoty opačné číslo (výraz).
Offline
#8 13. 10. 2011 18:59 — Editoval ((:-)) (13. 10. 2011 19:06)
Re: Definiční obory funkcí
↑ tesarin:
1 Hľadáš čísla menšie (prípadne rovné) ako -2 a súčasne menšie (prípadne rovné) ako 7
2


A znova hľadáš čísla s obidvoma vlastnosťami
3

Keď vyriešiš, znova hľadáš spoločné čísla.
Offline
#10 13. 10. 2011 19:18 — Editoval ((:-)) (13. 10. 2011 19:19)
Re: Definiční obory funkcí
↑ tesarin: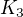 mi vyšlo
mi vyšlo 
Potom treba urobiť zjednotenie všetkých troch intervalov, lebo x môže patriť do hociktorého z nich, teda do  alebo do
alebo do 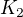 alebo do
alebo do 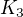 .
.

Interval je na strane nekonečna vždy o t v o r e n ý.
Offline
#12 13. 10. 2011 19:35
Re: Definiční obory funkcí
Offline
#14 13. 10. 2011 19:40
Re: Definiční obory funkcí
↑ tesarin:
Už to tak vyzerá ... :-)
Pre krajné hodnoty intervalov dostávaš po dosadení 0 ...
Offline






 - je to tak?
- je to tak? 


 - je to tak?
- je to tak?



 - je to tak?
- je to tak?








