Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 16. 10. 2011 11:53

Rufus
Příspěvky: 277
Reputace:   0 
 

dvojný integrál - křivka

$f(x,y) = xy$  $\Omega: y^2=2x ; x=2$

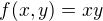
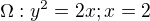
Podle podmínek mně vyšla parabola (počátek v 0 do +nekonečna) a čára rovnoměrná s osou y procházející dvojkou.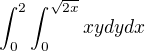

$\int_0^2 \int_0^{\sqrt{2x}} xy dydx$ Po úpravě mně vyšlo $\frac83$

Ještě ale nevím, jestli výsledek nemám vynásobit ještě 2, protože sem počítal jen oblast nad osou x a nevím jestli k tomu nemám přípočítat i oblast pod osou x.

Offline

  • (téma jako vyřešené označil(a) Rufus)

#2 16. 10. 2011 12:14

jelena
Jelena
Místo: Opava
Příspěvky: 30020
Škola: MITHT (abs. 1986)
Pozice: plním požadavky ostatních
Reputace:   100 
 

Re: dvojný integrál - křivka

Zdravím,

ano celková oblast vznikne vynásobením 2. Podrobně jsem nekontrolovala, ale zdá se být "mezivýsledek 8/3" v pořádku.

Offline

 

#3 16. 10. 2011 12:27

Rufus
Příspěvky: 277
Reputace:   0 
 

Re: dvojný integrál - křivka

↑ jelena:
Děkuji

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson