Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 10. 2011 14:36
Limita
Dobry den, mam potiz s jednou limitou bez L`Hospitala, ve skole zatim delame bez lhospitala a pomoci nej nemam tuto limitu problem vyresit, ale bez nej je to trochu problem.
Zadani:
Muj postup:
Mame neurcitost tvaru  , jako pomucku nam ucitel napsal pouzit zname limity pro
, jako pomucku nam ucitel napsal pouzit zname limity pro  , takze jsem se
, takze jsem se  snazil upravit do tvaru
snazil upravit do tvaru  , coz se mi take povedlo, vyslo mi, ze
, coz se mi take povedlo, vyslo mi, ze  , po dosazeni do limity a upraveni exponentu mi vychazi, ze:
, po dosazeni do limity a upraveni exponentu mi vychazi, ze: a po zlhopitalovani celkem lehce vyjde, ze ten exponent se rovna nule, ale jak to udelat bez lhospitala? mel jsem postupovat jinak?
a po zlhopitalovani celkem lehce vyjde, ze ten exponent se rovna nule, ale jak to udelat bez lhospitala? mel jsem postupovat jinak?
Diky.
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
- (téma jako vyřešené označil(a) Phate)
#2 16. 10. 2011 15:12
Re: Limita
Ahoj ↑ Phate:,
Neda sa vyuzit ze ?
?
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 16. 10. 2011 16:17 — Editoval vanok (17. 10. 2011 13:16)
Re: Limita
↑ Phate:
Aha ty pozeras na upravene formy.
A ja na tu prvu
mocniny okolo nuly su co?
a tak na co si komplikovat zivot?
Vratim sa vecer, napis tu zatial co si urobil
PRIDAVOK O 23 00, 16/10/2011
Moja myslienka je sa dat najprv do okolia nuly vdaka substitucii 
Ta tvoja otazka sa premeni na 
Ak pouzijes tieto dve lahko dokazatelne limity

lahko dojdes k vysledku
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 16. 10. 2011 20:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ Phate:
Zdravím,
proč jste neuvažovali přepis na  ? V tomto případě sice musím rozebrat pi/2 zleva a zprava, ale vychází mi v exponentě "nekonečno"*0 (což by mělo být 0).
? V tomto případě sice musím rozebrat pi/2 zleva a zprava, ale vychází mi v exponentě "nekonečno"*0 (což by mělo být 0).
Nevím, jestli jsem něco nepřehlédla (nebo zda něco nenabízí oblíbený autor s kolektivem - hledáno v MatWiki na klíčové slovo Rychlokurz).
Offline
#10 16. 10. 2011 20:33
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ Phate:
jak se vybrusluje okem? Touto cestou bych nemusela používat l´Hospital.
e-kova limita se rozumí "2. pozoruhodná"?
Offline
#12 16. 10. 2011 20:57
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita
Dobrý večer přeji,
předem se omlouvám, nemám po ruce papír, takže neručím za správnost, beru to nějak po paměti.
Po úpravě na limitu s exp bych použil jednu z pozoruhodných limit (tu s logaritmem) a dostal se postupně až na tebou zmíněné (bez exp, ať to mám stručnější):
Všimni si dvou věcí:
1) K úpravě jsem se dostal bez nutnosti "odhadovat" funkci ve tvaru y + 1/y, ale za pomocí standardních postupů. To není výtka, jen to může občas pomoci, ve chvilkách nesnází.
2) Schválně jsem neroznásobil závorku v čitateli, protože teď již snad vidíš, jak se úloha dopočítá. Stačí rozšířit jmenovatelem a výsledek je na světě. Nezapomeň na to, že funkce * (funkce s limitou nula) nemusí být vždy nula, ale je třeba to trochu okomentovat (případně to upravíš jako (1/2) sin 2x a nemusíš řešit tuto poznámku).
Zdravím.
Offline
#13 16. 10. 2011 21:19 — Editoval Phate (16. 10. 2011 21:19)
Re: Limita
↑ halogan:
Ahoj, mam par otazek:
...bych použil jednu z pozoruhodných limit (tu s logaritmem)...
myslis  nebo
nebo  nebo nejakou jinou?
nebo nejakou jinou?
Stačí rozšířit jmenovatelem a výsledek je na světě
Vysledek tak vyjde, ale je to evivalentni uprava, kdyz rozsirim vyrazem, kterej je v podstate nula?
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#14 16. 10. 2011 21:31
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita
↑ Phate:
Ahoj,
1) ad limita: myslím to druhé, to první ani není limita, jen přepis výrazu (který platí jen někdy, pozor na to).
2) ad rozšíření: "v podstatě" v matematice neplatí :-) My řešíme limitu na prstencovém okolí pí/2, a tam nikde cos x nulový není.
Offline
#15 16. 10. 2011 21:43
Re: Limita
↑ halogan:
Asi uz je na me moc pozde, ale jak se uplatni  v
v  ?
?
Jinak zatim smele vstrebavam jen se roji otazky, diky moc za pomoc :)
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#16 16. 10. 2011 21:48
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita
Řešíme limitu (exp opět neuvádím, to se ošetří bokem): ,
,
kde ten zlomek na konci vyhodíme přes aritmetiku limit. Dále jej zpracujeme pomocí pozoruhodné limity + věty o limitě složené funkce.
---
Nevím, na jaké jsi škole, tak nevím jak výrazně mám zacházet do detailů, jak moc si mohu dovolit opomíjet věci a tak.
Offline
#17 16. 10. 2011 22:00
Re: Limita
↑ halogan:
Studuju aplikovanou matematiku a chodil jsem dost dobry matematicky gympl, takze toho vstrebam celkem dost, jen limity na stredni u nas byly jen s jednou tou "pozoruhodnou" limitou a to  a pak ta uprava
a pak ta uprava  a vetsina uprav byly upravy z nedef. vyrazu na tvar
a vetsina uprav byly upravy z nedef. vyrazu na tvar  nebo
nebo  a pak lhospitalovat dokud nepojdem hladem, takze tohle hledani tech pozoruhodnych limit ve vsem je pro me trochu nove.
a pak lhospitalovat dokud nepojdem hladem, takze tohle hledani tech pozoruhodnych limit ve vsem je pro me trochu nove.
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#18 16. 10. 2011 22:03
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita
↑ Phate:
O tvých znalostech pochybnosti nemám, přeci jen tvé odpovědi zde čtu. Šlo mi spíše o to, co je od vás vyžadováno a na co bych měl upozornit. Takovou limitu lze spočítat na půl řádku, ale taky na půl strany :-)
Offline
#19 16. 10. 2011 22:09
Re: Limita
↑ halogan:
Spis mi jde o to, jestli v tom hledat donekonecna nejakou silenou upravu a nebo proste pouzit toho lhospitala, kterej to vyresi jednim krokem, ale to pouziti tech pozoruhodnych limit se mi velmi libi. Oznacim za vyresene a diky za reakce.
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#20 16. 10. 2011 22:19
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita
↑ Phate:
Promiň mi narušení vyřešeného tématu, jen musím něco dodat:
Ono to není tak snadné, nelze prostě na zlomek hodit L'Hospitala, usmát se a dopočítat to. I L'H má určité předpoklady, které nejen že jsou občas obtížné na kontrolu, ale často jsou i nesplněné.
Pokud si na tabulkové limity zvykneš, tak už ty úpravy uvidíš v hlavě, ono to je docela intuitivní. Uvedu příklad:
Máme ty limity, kde sinx/x, tgx/x, arctg/x, logx/(x-1), (1-cosx)/x^2 + jejich inverze, jdou všechno někde k jedničce/jedné polovině nebo tak něco. Můžeš si tedy říci, že limitně kolem nuly se sinx "chová" jako x, stejně tak se x^2/2 chová jako 1-cosx atp. V hlavě si tedy tyto výrazy začneš nahrazovat, a hned se to začne rýsovat.
Popsat to vše formálně beru jako samozřejmost.
Podobné hlavoúpravy pak jdou aplikovat třeba u řad.
Offline
#21 17. 10. 2011 13:06
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ vanok:
děkuji za přidaný postup :-) ještě je dobré sdělit, že je přidán.
↑ Ondřej:
děkuji :-) teď jsem zjistila, že je to Demidovič č. 523 (tedy jen pro vyvolené), ↑ můj postup: by skutečně byl na půlřadku (ale bez l´Hospital).
---------------------------------------
Ale s hledáním na MatWiki by se něco podniknout mělo - a umístit Rychlokurz na stránku VŠ (a když už budete u toho, tak UJČ má upravu adresy - také prosím opravit do slovníku), mně se ještě teď třepe ruka po opravě příspěvku váženého Moderátora :-)
Děkuji a zdar přeji.
Offline
#22 17. 10. 2011 13:17
Re: Limita
Ahoj ↑ jelena:,
Dakujem za upozornenie, pripisal som jasne do mojej zpravy kedy to bolo priadane
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#24 17. 10. 2011 13:27
Re: Limita
Ahoj Phate
Este mala otazka.
Pises
Phate napsal(a):
takze jsem se
snazil upravit do tvaru
, coz se mi take povedlo, vyslo mi, ze
, .
Mozes to dokazat?
Dakujem
Srdecne vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
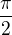
 nebo ne?
nebo ne?