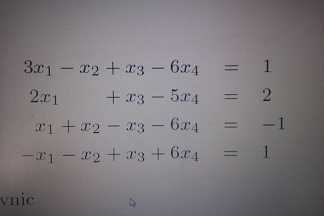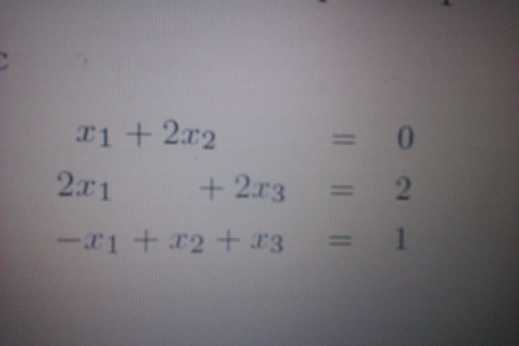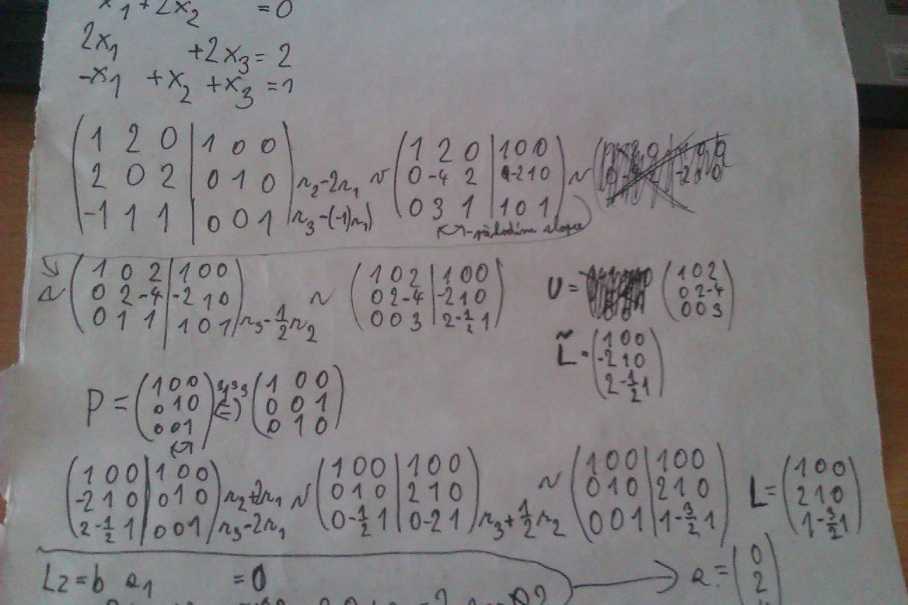Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 10. 2011 12:10
Re: řešení soustavy lineárních rovnic
↑ georgeo4:
Šak áno. Ten posledný riadok sa ti skutočne vynuluje. Čo to teda znamená? ...
Offline
#3 18. 10. 2011 12:13 — Editoval georgeo4 (18. 10. 2011 12:14)
Re: řešení soustavy lineárních rovnic
↑ standyk: No jo vynulu je se mi ale co dál jak dojít k tomu výsledku? Jo vím že to má nekonečně mnoho ešení :) nevím co jse děje ikdyž je to asi lehké já mám dny kdy to nedokážu vypočítat :D já bych udělal něco s parametrem ale zase mám to svoje ale :)
Offline
#4 18. 10. 2011 12:22 — Editoval standyk (18. 10. 2011 12:26)
Re: řešení soustavy lineárních rovnic
↑ georgeo4:
Na tých rovniciach vidno že 4. riadok je -1 násobkom tretieho. Teda ten štvrtý môžeš skutočne vynulovať. Máš teda 3 rovnice o 4 neznámych. Z toho teda plynie že bude mať nekonečne veľa riešení a budeš musieť skutočne použiť parameter. Upravuj tak ako keď normálne riešiš a keĎ sa dopracuješ k nejakej jednej rovnici o 2 neznámych. Jednu neznámu si vyjadri pomocou druhej. Napr. keby ti vzniklo: 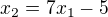 tak potom ostatné neznáme x3 a x4 taktiež vyjadríš pomocou x_1.
tak potom ostatné neznáme x3 a x4 taktiež vyjadríš pomocou x_1.
Tým sa stane to x1 parameter a dostaneš riešenie napr. že riešenie bude usporiadaná štvorica, kde v jednotlivých členoch bude vystupovať parameter 
Offline
#5 18. 10. 2011 12:29
Re: řešení soustavy lineárních rovnic
A ještě jestli můžu jestli že mám matice (3A-2B)Cna-1 * vektor u
Chci se zeptat normálně vynásobím 3* matici a a odečtu 2* matici B Poté vynásobím inverzní maticí C a pak vynásobím vektorem u je postup správně nemám nejdříve vynásobit Inverzní matici c s vektorem a pak až s závorkou ? :) diky
Offline
#6 18. 10. 2011 12:39 — Editoval standyk (18. 10. 2011 12:54)
Re: řešení soustavy lineárních rovnic
↑ georgeo4:
Najprv si roznásob zátvorku , vynásob s inverznou maticou C a potom s vektorom u. Násobenie je komutatívne, ale násobenie matíc komutatívne nie je.
Offline
#8 18. 10. 2011 14:45
Re: řešení soustavy lineárních rovnic
↑ georgeo4:
Mně to tedy vychází jinak
Můžeš si to zkontrolovat Tady
Offline