Matematické Fórum

Jenda1996 · 07. 05. 2007 10:39

Dobrý den,poradil by me někdo případne spočítal přiklad:

Je dán kruh o poloměsu s.Z kruhové výseče o středovém úhlu o velikosti alfa je svinut kuželový filtr.Rozhodněte ,jak je třeba zvolit alfa,aby tento filtr měl maximální objem.

Děkuji předem za pomoc.
Jenda

jelena · 07. 05. 2007 21:29

poslu mailem, nebot se hrozne nadru, nez to vypisi.
V podstate budeme hledat maximum funkce uhlu alfa, takze na zaver budeme derivovat.
Ale nejdriv musime vytvorit funkci - vzorecek pro objem kuzele umime, budeme hledat polomer zakladny a vysku kuzele pres zadane alfa a polomer puvodniho kruhu.
Tak zacneme, tedy alespon cast z nas:-) .

Jenda1996 · 08. 05. 2007 16:46

Dobrý den Jeleno,
jsem velice rád že jste se rozhodla mě s tímto příkladem pomoct ale bohužel jsem slibovaný email nedostal.
Mohl bych Vás poprosit o jeho zaslání znovu.Uvedu pro jistotu i svoji druhou adresu.
Ještě jednou Vám moc děkuji,velice jste mě pomohla.
S pozdraven
Jenda

Jenda1996@seznam.cz
jenda.petera@seznam.cz

jelena · 08. 05. 2007 18:44

uz je to zaslano, doslo OK?

Jenda1996 · 08. 05. 2007 19:25

jelena napsal(a):
uz je to zaslano, doslo OK?

Dobrý den pani Jeleno,
děkuji Vám za vaši rychlou odpověď přišlo to vpořádku,moc jste mě pomohla.
Všiml jsem si ,že pomáháte i jiným ,takové lidi obdivuji ,dnes už jich moc není.
S pozdravem

Jenda

lipca · 23. 05. 2007 18:09

Byl by jeden z Vás prosím tak hodný a poslal mi to taky na lipcacz@seznam.cz? Diky moc

jelena · 23. 05. 2007 19:46

uz to letelo :-)

Kondr · 24. 05. 2007 10:08 — Editoval Kondr (25. 05. 2010 02:01)

Pro pripad, ze by se tu objevil jeste nekdo, koho zajima reseni (at se to nemusi vzdy posilat mailem)
Pro vysku kuzele v, polomer podstavy r a vzdalenost s plati
$v^2+r^2=s^2$ , objem kuzele je
$\frac{\pi}{3}vr^2=\frac{\pi}{3}v(s^2-v^2)$ .
Vazeny aritmeticky prumer cisel $s^2-v^2$ a $2v^2$ s vahami 2/3 a 1/3 je $\frac{2}{3}s^2$ , jejich vazeny geometricky prumer (se stejnymi vahami) je $\sqrt[3]{\sqrt{2}v(s^2-v^2)}^2$ . Maximalizovat objem tedy znamena maximalizovat tento geometricky prumer, ten ale muze byt roven nejvyse aritmetickemu a to prave kdyz jsou prumerovana cisla stejna, tedy
(1) $s^2-v^2=2v^2$ ,
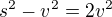po dosazeni 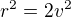$r^2=2v^2$ ,
$r=\sqrt{2}v$ .
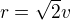Navic z (1)
$s=\sqrt{3}v$ ,
takze $r=\sqrt{2/3}s$ .
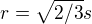V kruhu o polomeru r odpovida podstavna kruznice uhlu $2\pi$ , takze v puvodnim kruhu odpovida uhlu
$\alpha=2\pi\sqrt{2/3}$ .

Doufam ze jsem neudelal zadnou chybu a ze jsem pomohl. Ten parser TeXu by to chtelo vazne nejakej interni :)

EDIT: Vzorce po třech letech restaurovány.

snaajk · 23. 04. 2015 19:07 — Editoval snaajk (23. 04. 2015 19:07)

jasny dik moc

BadInMath · 23. 11. 2016 19:43

↑ Kondr:
Ahoj, vím že je to strašně staré. Asi je to velmi hloupé a omlouvám se za to, ale mohl bych se zeptat z čeho se udělal ten aritmetický průměr a kde se vzalo $2v^2$ ? A ještě k čemu je u úlohy důležitý ten geometrický průměr?

Jestli si toho někdo všimne tak děkuji za případnou pomoc :)

BadInMath · 23. 11. 2016 21:40

Tak jsem si nakonec poradil, omlouvám se za spamy. Zdejší řešení pomohlo, díky :)

Matematické Fórum

#1 07. 05. 2007 10:39

Jak najít maximální objem kuželu?

#2 07. 05. 2007 21:29

Re: Jak najít maximální objem kuželu?

#3 08. 05. 2007 16:46

Re: Jak najít maximální objem kuželu?

#4 08. 05. 2007 18:44

Re: Jak najít maximální objem kuželu?

#5 08. 05. 2007 19:25

Re: Jak najít maximální objem kuželu?

jelena napsal(a):

#6 23. 05. 2007 18:09

Re: Jak najít maximální objem kuželu?

#7 23. 05. 2007 19:46

Re: Jak najít maximální objem kuželu?

#8 24. 05. 2007 10:08 — Editoval Kondr (25. 05. 2010 02:01)

Re: Jak najít maximální objem kuželu?

#9 23. 04. 2015 19:07 — Editoval snaajk (23. 04. 2015 19:07)

Re: Jak najít maximální objem kuželu?

#10 23. 11. 2016 19:43

Re: Jak najít maximální objem kuželu?

#11 23. 11. 2016 21:40

Re: Jak najít maximální objem kuželu?

Zápatí