Matematické Fórum

pumping_lemma · 22. 10. 2011 23:47

Ahoj, mam otazku k nasledujucemu vypoctu:

http://www.math24.net/calculation-of-vo … grals.html

Pri ratani objemu kuzela zistili ze je ohraniceny povrchom 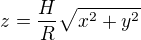$z=\frac HR \sqrt{x^2 + y^2}$

moze mi prosim niekto objasnit ako sa k tomu dostali? dakujem

Olin · 23. 10. 2011 00:02

Asi takto: kdyby to bylo $z = \sqrt{x^2 + y^2}$ , byl by to kužel, který vznikne rotací pravoúhlého rovnoramenného trojúhelníka (protože $\sqrt{x^2+y^2}$ je vzdálenost od počátku). No ale protože ten trojúhelník není v obecném případě rovnoramenný, ale má strany (odvěsny) o délkách $H$ a $R$ , bude to $z = \tfrac HR\sqrt{x^2 + y^2}$ (poměr $\tfrac HR$ udává, jak "rychle" roste $z$ v závislosti na vzdálenosti od počátku).

Matematické Fórum

#1 22. 10. 2011 23:47

Objem kuzela cez trojny integral

#2 23. 10. 2011 00:02

Re: Objem kuzela cez trojny integral

Zápatí