Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Tranzitivní uzávěr (TOTO TÉMA JE VYŘEŠENÉ)
#1 25. 10. 2011 00:03
Tranzitivní uzávěr
Zítra píšu písemku na relace a narazil jsem na jednu nejasnost.
Mám příklad: Mějme množinu  a relaci
a relaci  ,
,  . Spočítejte všechny mocniny této relace nutné pro zisk jejího tranzitivního uzávěru
. Spočítejte všechny mocniny této relace nutné pro zisk jejího tranzitivního uzávěru
Já bych to řešil tak, že bych postupně doplnoval prvky do relace abych splnil pravidlo tranzitivity:  , jenomže tady se to chce nějakým umocňováním relace a vůbec nevím, co si pod tím představit.
, jenomže tady se to chce nějakým umocňováním relace a vůbec nevím, co si pod tím představit.
Děkuji za každou radu
Navštivte portál Matematika pro každého! http://maths.cz
Offline
- (téma jako vyřešené označil(a) Blujacker)
#2 25. 10. 2011 16:10 — Editoval Rumburak (25. 10. 2011 16:14)
Re: Tranzitivní uzávěr
↑ Blujacker:
Transitivita relace R se dá popsat podmínkou  , kde
, kde  je operace skládání relací. Proto ty "mocniny"
je operace skládání relací. Proto ty "mocniny"
( můžeme zapsat jako
můžeme zapsat jako 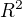 ).
).
Offline
#3 25. 10. 2011 16:12
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Tranzitivní uzávěr
↑ Blujacker:
Umocňování relace je zhruba toto (definováno induktivně):
Neboli: R^2 je množina všech možných "složení" dvou navazujících "šipek" relace (načrtni si to na konečné relaci a snad to bude jasné), R^3 je to stejné, akorát beru vždy prvně šipku z R^2 a k ní šipku z R atd. Nebo si lze libovolnou šipku z R^3 také představit jako tři po sobě navazující šipky (toto s šipkami těžce neformálně, jen tak pro představu).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#4 26. 10. 2011 13:14
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Tranzitivní uzávěr (TOTO TÉMA JE VYŘEŠENÉ)