Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Kompakty v Sorgenfreyově přímce
#1 10. 08. 2011 16:53
Kompakty v Sorgenfreyově přímce
Dokažte, že každá kompaktní podmnožina Sorgenfreyovy přímky je nejvýše spočetná.
(Sorgenfreyova přímka je 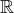 s topologií generovanou intervaly
s topologií generovanou intervaly 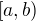 pro
pro  .)
.)
Offline
#2 22. 08. 2011 15:08 — Editoval Rumburak (23. 08. 2011 10:47)
Re: Kompakty v Sorgenfreyově přímce
Offline
#3 22. 08. 2011 22:06
Re: Kompakty v Sorgenfreyově přímce
↑ Rumburak:
Jde ovšem skutečně o důkaz spočetnosti pro kompaktní podmnožiny? Přijde mi, že bylo dokázáno, že každá sekvenciálně kompaktní podmnožina je spočetná. Nejsem si jistý, jestli to už pro Sorgenfreyovu přímku postačuje.
Offline
#4 23. 08. 2011 10:00 — Editoval Rumburak (23. 08. 2011 10:41)
Re: Kompakty v Sorgenfreyově přímce
↑ Olin:
A jo, neuvědomil jsem si, že v topologii (narozdíl od analýzy v 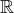 ) kompaktnost není definována stejně jako sekvenciální kompaktnost,
) kompaktnost není definována stejně jako sekvenciální kompaktnost,
takže jsem vlastně dokazoval tvrzení, že každá sekvenciálně kompaktní část Sorgenfreyovy přímky je nejvýše spočetná (dokončení důkazu
sestrojením rostoucí posloupnosti z prvků nespočetné podmnožiny už je mi také jasné).
Ještě se nad tím zamyslím.
Offline
#5 28. 10. 2011 11:02
Re: Kompakty v Sorgenfreyově přímce
↑ Olin:
Nejake riesenie je tu: http://www.mymathforum.com/viewtopic.php?f=22&t=81
Netusim, aku zivotnost bude mat ta linka, tak to sem skopirujem:
Offline
Stránky: 1
- Hlavní strana
- » Zajímavé úlohy z matematických struktur
- » Kompakty v Sorgenfreyově přímce
 značí Sorgenfreyovu přímku dle výše uvedené definice. Všechny níže uvažované topologické pojmy (okolí, limita,
značí Sorgenfreyovu přímku dle výše uvedené definice. Všechny níže uvažované topologické pojmy (okolí, limita, je konvergentní posloupnost v
je konvergentní posloupnost v 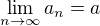
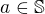 . Zvolme
. Zvolme  . Potom množina
. Potom množina 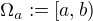
 . Z (1) plyne, že výrok
. Z (1) plyne, že výrok  a tím spíše výrok
a tím spíše výrok  (dle (2))
(dle (2)) kompaktní množina v
kompaktní množina v 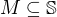 by snad (?) nemělo být obtížné sestavit nekonečnou rostoucí posloupnost -
by snad (?) nemělo být obtížné sestavit nekonečnou rostoucí posloupnost - (na přání to kdyžtak zkusím doplnit),
(na přání to kdyžtak zkusím doplnit), 