Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 28. 10. 2011 15:24 — Editoval Jenda358 (28. 10. 2011 15:25)
Re: limita
↑ Jenda358:
Pokud ano, nejdříve bych přepsal podíl odmocnin na odmocninu podílu, tedy .
.
Dále můžeme využít toho, že za jistých předpokladů (které jsou zde splněny) se limita odmocniny rovná odmocnině limity, tedy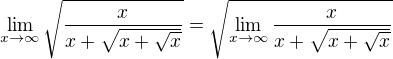 .
.
Dále už stačí vytknout v čitateli i jmenovateli  , zkrátit a dopočítat.
, zkrátit a dopočítat.
Offline