Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 07. 2008 20:36 — Editoval ttopi (17. 07. 2008 20:37)
Aplikace Diferenciálního počtu
Zdravím vespolek.
Až teď jsem zjistil, že jsme ve škole něco zanedbali (nevím proč).
Chci si počítat příklady typu, které vidítě dole. Bohužel jsme ve škole nevypočítali ani jeden příklad takového typu a ačkoli to asi nebude nic extra těžkého, chybí mi početní praxe příkladů tohoto typu.
Prosím proto hodnou duši, která mi zde napíše postup i s komentářem :-)
Zároveň to pro vás může být taková rozvička :-)
Příklad1:
Najděte válec, který má při daném objemu minimální povrch.
Příklad 2:
Do kružnice s polomerem r vepište rovnostranný trojúhelník maximálního obsahu.
Příklad 3:
Dvě chodby široké 2,4 m a 1,6 m se protínají pod pravým úhlem. Určete délku nejdelšího žebříku, který lze ve vodorovné poloze přenést z jedné chodby do druhé..
Příklad 4:
Kouli o poloměru r je vepsán kvádr se čtvercovou podstavou maximálního objemu. Určete jeho rozměry.
Poprosím o opravdu komentovaný postup s výpočtem. Odkazy na podobné příklady si samozřejmě mohu najít sám. Tak do toho :-)
oo^0 = 1
Offline
#2 17. 07. 2008 23:24
Re: Aplikace Diferenciálního počtu
to ttopi
Príklad 1. Obdobný sa riešil nedávno tu: http://forum.matweb.cz/viewtopic.php?id=3329&p=4 , je to to isté čo ten tvoj, ibaže na konci sú dosadené čísla. Myslím, že je to tam dos? podrobne popísané. Inak ty si tú úlohu zadával:).
Príklad 2.: Neviem či mi to už nemyslí, alebo je tam nejaká chyba ale do kružnice vieme vpísa? rovnostranný trojuholník iba s jedným obsahom nie? a jeho stranu a výšku nie je problém vvypočíta? podľa goniometrických funkcií.
You know who
(or maybe not)
Offline
#3 17. 07. 2008 23:49
Re: Aplikace Diferenciálního počtu
Príklad č.3
| |
| |
| |
| | <-- chodba o šírke 1,6 m
| |
| |
| |
|\ |
| \ |
|_\|_____________________________
| \
|_ \______________________________
^ ^
| |
rebrík chodba o šírke 2,4m
rebrík zviera s chodbou o šírke 2,4m rovnaký uhol alfa ako s kolmicou na chodbu o šírke 1,6m. Jeho dĺžku x vypočítame: 
Tento vvzorec vyjadruje závyslos? dĺžky rebríka iba na uhle alfa. Pomocou derivácie tejto fc musíme nájs? maximum tejto funkcie.
Týmto som si pomerne istý, nasledujúcim tak na 80%
Táto derivácia sa musí rovna? nule, teda dostávame:  . Hmm... to ma akosi teraz nenapadá ako vyrieši?. No ak by sme mali uhol alfa, tak dopočíta? dĺžku rebríka by už nebol problém.
. Hmm... to ma akosi teraz nenapadá ako vyrieši?. No ak by sme mali uhol alfa, tak dopočíta? dĺžku rebríka by už nebol problém.
You know who
(or maybe not)
Offline
#4 18. 07. 2008 07:28
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Aplikace Diferenciálního počtu
↑ matoxy:
Bývá to často v učebnicích, jenom trochu jinak formulované: plavební kanál místo chodby a kláda kterou je potřeba splavit místo žebříku. Určitě by se to dalo dohledat v literatuře.
---------------------------------------------------------------------
Kája poskakoval vedle tatínka a zdál se býti podle jeho vysoké, statné postavy, jako hříbeček pod doubkem. Jenže nebyl tak nehybný jako hříbeček.
Jak se ukázala věž kostela, zastavil se Kája: „Tati, já tam přece nepůjdu! Pojďte, vrátíme se! Mamince je beztoho doma smutno. Já tam ve škole nevydržím sedět!“
Offline
#5 18. 07. 2008 08:47
Re: Aplikace Diferenciálního počtu
Tak úloha s žebříkem je vyřešena.
Derivace je rovna 0 pro 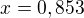 , tedy pro nějakých
, tedy pro nějakých  .
.
Pak po dosazení do funkce dostaneme přibližně 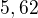 ,což je přibližná maximální délka žeříku, který by měl jít protáhnout z jedné chodby do druhé :-)
,což je přibližná maximální délka žeříku, který by měl jít protáhnout z jedné chodby do druhé :-)
Díky moc za pomoc, ale příkladů tu ještě pár je, tak do toho :-)
oo^0 = 1
Offline
#6 18. 07. 2008 09:15
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Aplikace Diferenciálního počtu
↑ ttopi:
Zdravim :-)
Ted nemam vice casu - mam na navsteve moji maminku (1,5 denni inspekce jednou za 5 let :-) Ale pridam systematicky navod :
Kazda uloha spociva v nalezeni funkce jedne promenne a ve vysetreni teto funkce na extremy (pomoci nastroju diferencialniho poctu). Daleko vetsi smysl (systematicky) ma umet sestavit tu funkci - spravne zvolit promennou a vysledny tvar funkce.
Proto by bylo dobre, vedet, zda problem cini sestaveni funkce (to bychom se meli vydat smerem k reseni slovnich uloh zejmena geometrickych a nedelat si starosti s diferencialnim poctem). Nebo opravdu vysetreni extremu.
OK?
Offline
#7 18. 07. 2008 09:28 — Editoval ttopi (18. 07. 2008 09:31)
Re: Aplikace Diferenciálního počtu
↑ jelena:
Ahoj:-)
Samozřejmě, maminká má vždycky přednost :-)
Jde o to, že třeba v 1.úloze není známo ani jedno číslo, tudíž když sestavím funkci pro povrch válce, jako to udělal vedle kolega Cheop, cituji: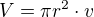 kde V - objem válce, r - poloměr válce, v - výška válce
kde V - objem válce, r - poloměr válce, v - výška válce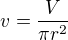
 - povrch válce - má být minimální
- povrch válce - má být minimální
Tak budu mít funkci S, ale v ní 2 proměnné, a sice r a V. A tady narazím.
oo^0 = 1
Offline
#8 18. 07. 2008 09:40 — Editoval Cheop (18. 07. 2008 09:45)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Aplikace Diferenciálního počtu
↑ ttopi:
V tom příkladu se píše:
Najděte válec, který má při daném objemu minimální povrch. Z toho tedy plyne, že objem je jakoby znám. (V)
Pomocí V určíš dvě proměnné r- poloměr válce a v - výšku válce tak, aby byl povrch S minimální.
A k tomu právě slouží diferenciální počet, protože pomocí první derivace určíš maximum nebo minimum a pomocí druhé derivace určíš stacionární body.
K příkladu 2.
Nemá být zadání toto?
Do kružnice s polomerem r vepište trojúhelník maximálního obsahu.
Podle mě pak vyjde, že ten trojúhelník je rovnostranný
Nikdo není dokonalý
Offline
#9 18. 07. 2008 09:50 — Editoval ttopi (18. 07. 2008 09:58)
Re: Aplikace Diferenciálního počtu
↑ Cheop:
To zadání je zkopírované, takže je přesné. Chce se po nás vyjádřit stranu a.
U té 1 jsem si trochu pomohl tím, že jsem si určil, že objem je 20. Pak mi vyšlo, že r musí být 1,47. Když je V 40, tak r musí být 1,85. Ale když je V neznámé, tak nevím, jak s ním mám počítat.
Správné řešení má být 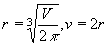 .
.
oo^0 = 1
Offline
#12 18. 07. 2008 10:47 — Editoval ttopi (18. 07. 2008 10:50)
Re: Aplikace Diferenciálního počtu
↑ Cheop:
To mám, ale nevím, jak to derivovat, když jsou tam 2 proměnné (r a V).
Jak říkám, když jsem si pomohl dosazením V, není problém, ale takto, nevim.
EDIT: Už to vidím. Problém byl v tom, že jsem špatně zderivoval zlomek, kde je V.Díky.
Jinak ten trojúhelník mi vyšel stejně. Zajímavé je, že se k tomu dá dospět i bez derivací. Když jsem sestavil funkci pro obsah vepsaného trojúhelníka v závislosti na poloměru kružnice, maximum bylo v nekonečnu.
oo^0 = 1
Offline
#13 18. 07. 2008 12:19 — Editoval Cheop (18. 07. 2008 12:28)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Aplikace Diferenciálního počtu
Příklad 4)
Označme: a - strana čtvercové podstavy
v - výška kvádru
V - objem kvádru - má být maximální
Musí platit: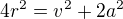 - tělesová úhlopříčka
- tělesová úhlopříčka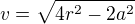

 derivujeme podle a a dostaneme:
derivujeme podle a a dostaneme: zkrátíme výrazem
zkrátíme výrazem a dostaneme:
a dostaneme: dopočteme výšku kvádru
dopočteme výšku kvádru

 jedná se o krychli
jedná se o krychli
Nikdo není dokonalý
Offline
#21 18. 07. 2008 16:50 — Editoval matoxy (18. 07. 2008 16:52)
Re: Aplikace Diferenciálního počtu
Kde mám teda v svojom postupe chybu? Lebo ja si ju tam neviem nájs?, ibaže by bola zlá samotná myšlienka ako som to počítal?
+ to Chrpa
Pre aký uhol a dosadením do akej rovnice ti vyšla dĺžka rebríka 5,618 m?
Editace: + mne vyšla dĺžka rebríka cez 8 metrov dosadením do tej mojej rovnice uhol alfa tých 33°.
You know who
(or maybe not)
Offline
#22 18. 07. 2008 16:56
Re: Aplikace Diferenciálního počtu
matoxy: Správně je oněch 49°.
Ty jsi mě nakopl správně, tak to sám doklepni. Zderivuj funkci pro délku přepony (vlastně žebříku) a polož rovno 0 - tím získáš úhel, pro který má funkce minimum. Pak dosadíš do funkce a dostaneš délku žebříku, 5,62m.
oo^0 = 1
Offline
#23 18. 07. 2008 18:53 — Editoval matoxy (19. 07. 2008 17:30)
Re: Aplikace Diferenciálního počtu
Editace: akosi stále neviem na to prís?, aká je funkcia pre dĺžku rebríka? Z Pytagorovej vety nemôžeme lebo nepoznáme ani stranu a ani b, nie? Potom ostávajú len goniometrické fc a tam ma napadá iba to, čo som napísal. Aká je teda tá funkcia?
You know who
(or maybe not)
Offline
#24 31. 07. 2008 21:29 — Editoval Chrpa (31. 07. 2008 22:06)
Re: Aplikace Diferenciálního počtu
Dostávám se k vysvětlení po delší době:
Podle obrázku musí platit:
Z podobnosti trojúhelníka platí:
 - úpravou:
- úpravou: rovnici derivujeme dle x a derivaci položíme rovnu nule
rovnici derivujeme dle x a derivaci položíme rovnu nule


![kopírovat do textarea $x=\sqrt[3]{a^2b}$](/mathtex/4f/4fe54b94e986dd1f4e59ac4f91307e3d.gif)
Pro náš případ pokud za a a b dosadíme dostaneme:
dostaneme: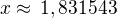 dopočteme y
dopočteme y teď už je možné dopočítat délku žebříku:
teď už je možné dopočítat délku žebříku:

Pokud bychom pokračovali v úpravách obecného vztahu pak bychom dospěli k délce:
Offline

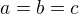 a dále
a dále
 pak
pak 

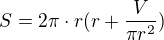
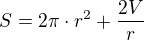 derivujeme podle r a derivaci položíme rovnu nule
derivujeme podle r a derivaci položíme rovnu nule
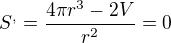

 , no aj tak neveim ako prís? na to kedy sa to rovná.
, no aj tak neveim ako prís? na to kedy sa to rovná.

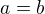 pak
pak
