Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 10. 2011 05:27 — Editoval vanok (02. 03. 2018 09:05)
najkrajsia teorema
Ktora matematicka teorema je podla vas najkrajsia?
Srdecne Vanok
Addendum.
Akoze povodny umysel nemal velky uspech, tak som ho trochu rozsiril, a pravidelne pridavam do tohto vlakna ( co mozte aj vy) zaujimave (podla mna) matematicke citania na ktore natrafim. ( A tie, iste casto obsahuju «najkrajsie » matematicke vety ... aspon si to myslim).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 16. 10. 2011 14:04
Re: najkrajsia teorema
Je ich vela peknych teorem, peknych vzorcov, peknych dokazov
Na inom fore som nasiel toto
Pre 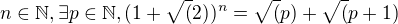
Pekne ze?
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 16. 10. 2011 18:56
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
↑ vanok:
Ahoj, máš na mysli krásu věty z pohledu jejího znění nebo z pohledu jejího důkazu?
"Máte úhel beta." "No to nemám."
Offline
#5 16. 10. 2011 22:02
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
vanok napsal(a):
Pre
Ahoj, máš i důkaz tohoto tvrzení? Vypadá samo velmi zajímavě. Nevím, zda je to nějaká deformace, ale teprve pěkný důkaz pro mě znamená i pěkné tvrzení. :-) Díky.
"Máte úhel beta." "No to nemám."
Offline
#6 16. 10. 2011 23:52 — Editoval vanok (16. 10. 2011 23:53)
Re: najkrajsia teorema
↑ check_drummer:
Ano dokazal som to, a je to ozaj jednoduche.
Mam ho hned dat sem alebo chcete mat radost hladat?
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 17. 10. 2011 16:15 — Editoval vanok (17. 10. 2011 21:30)
Re: najkrajsia teorema
Ahoj ↑ check_drummer:
Ziadny pokus na dokaz?
Dobre ja naznacim ako som to ja robil
Najprv som napisal niekolko prvych 
v forme 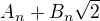 a samozrejme aj zkontroloval tu nasu "konjekturu ci domienku"
a samozrejme aj zkontroloval tu nasu "konjekturu ci domienku"
To pozorovanie mi podarilo "uhadnut" jednu rekurentnu relaciu z troma clenmy....
A to som overil indukciou ... a sedelo to.
Ak chces redigujem ti to tu.
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 20. 10. 2011 19:24
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
↑ vanok:
Ano, důkaz indukcí je jednoduchý. Jen jsem předtím neměl čas ho provést. :-)
Je to tvrzení zajímavé tím co říká - důkaz však už moc nápadu nemá. :-)
"Máte úhel beta." "No to nemám."
Offline
#10 20. 10. 2011 19:47
Re: najkrajsia teorema
↑ Olin:
↑ check_drummer:
Nevahajte z vasimy dokazmy. Ja doplnim moj len co budem mat trochu casu
A tesim sa na dalsich vela peknych teorem, peknych vzorcov, peknych dokazov
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 20. 10. 2011 19:49 — Editoval vanok (23. 10. 2011 01:03)
Re: najkrajsia teorema
↑ Olin:
Ano vidim je to evidentne.
:-)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 27. 10. 2011 14:11 — Editoval vanok (27. 10. 2011 14:12)
Re: najkrajsia teorema
↑ Olin:,nevahaj a daj nam tu tvoj dokaz.
Ja potom doplnim ten moj povodny...
A vsetci foristy:
Nevahajte tu dat to co je podla vas najkrajsia teorema, najkrajsi vzorcec, najkrajsi dokaz.
Pridavam dalsiu tehlicku: Niektore z dokazov ze MNOZINA PRVOCISIEL JE NEKONECNA
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 29. 10. 2011 22:34 — Editoval vanok (01. 11. 2011 11:50)
Re: najkrajsia teorema
↑ vanok:
prvy dokaz
vety <<MNOZINA PRVOCISIEL JE NEKONECNA>>
a asi aj taky co kazdy pozna
Ak to nie je pravda ze mnozina vsetkych cisiel je nekonecna , tak mame konecny pocet N prvocisiel 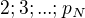 ,
,
Potom cislo  , nie je delitelne zo ziadnym prvocislom z nasho zoznamu.
, nie je delitelne zo ziadnym prvocislom z nasho zoznamu.
Tak  je prvocislo ale nie je v nasom zozname.
je prvocislo ale nie je v nasom zozname.
To je kontradikcia z tym ze mame konecny pocet N prvocisiel.
Zda sa vam pekny?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 01. 11. 2011 11:02
Re: najkrajsia teorema
Dnes ziadna pekna teorema
ale adresa na Webe
http://hermay.org/jconstant/wasan/sangaku/index.html
Reagujte. Hladajte. Rieste ...
Sangaku je nakazlive?
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 01. 11. 2011 11:41 — Editoval Pavel Brožek (01. 11. 2011 11:41)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: najkrajsia teorema
↑ vanok:
Jen bych poopravil, že M není nutně prvočíslo, ale je nutně dělitelné nějakým prvočíslem různým od prvočísel  (značím
(značím 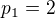 a tak dále). (Např. pro
a tak dále). (Např. pro 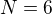 je
je  .)
.)
Offline
#16 01. 11. 2011 11:54 — Editoval vanok (01. 11. 2011 12:02)
Re: najkrajsia teorema
↑ Pavel Brožek:
Ano to mas pravdu ze takyto vyraz neda vseobecne prvocislo.Ale to je iny problem.
Toto ta moze zaujimat http://oeis.org/A006862
Ale ja som napisal  , kde v sucine su VSETKY prvocisla....
, kde v sucine su VSETKY prvocisla....
lebo som vychadzal z predpokladu ze je ich len konecny pocet.
Srdecne Vanok
PS opravil som v mojom prispevku malu chybu nepozornosti
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 01. 11. 2011 12:12 — Editoval Pavel Brožek (01. 11. 2011 12:13)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: najkrajsia teorema
↑ vanok:
Máš pravdu, špatně jsem si to rozmyslel a hledal jsem spor jinde. Už je mi jasné, že M je prvočíslo, pokud předpokládáme, že je prvočísel jen konečný počet.
Teď se mi zdá důkaz hezčí :-).
Offline
#18 01. 11. 2011 12:45
Re: najkrajsia teorema
↑ vanok:
Amatery geometrie, este nieco o SANGAKU
http://www.its.caltech.edu/~ilian/ma1c/temple.pdf
Zaujimavy clanok z Scientific American May 1998
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 01. 11. 2011 17:23
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
Pro důkaz nekonečnosti prvočísel jsem založil téma:
http://forum.matweb.cz/viewtopic.php?id=35867
Jeho tvrzení má interpretaci: mezi čísly 1 až 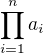 pro
pro  existuje číslo, které není násobkem žádného
existuje číslo, které není násobkem žádného  . Což pokud jako
. Což pokud jako  zvolíme prvočísla znamená, že mezi 1 až
zvolíme prvočísla znamená, že mezi 1 až 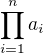 existuje ještě nějaké další prvočíslo.
existuje ještě nějaké další prvočíslo.
Ovšem důkaz toho tvrzení nesmí být založen na této interpretaci, jinak ho nelze použít k důkazu nekonečného počtu prvočísel. :-))
"Máte úhel beta." "No to nemám."
Offline
#20 01. 11. 2011 17:37
Re: najkrajsia teorema
↑ check_drummer:
To pises mne?
Dokaz co som napisal je od Euclida!
À dokonale funguje
A tu inu otazku sme uz vyriesili.
↑ check_drummer: inac si pisal ze mas dokaz, na predoslu temu, Tak nevahaj. Napis ho sem.
Z radostou sa pozriem na tvoj pripevok.
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 01. 11. 2011 18:58
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
↑ vanok:
Ten příspěvek jsem psal všeobecně všem, kdož čtou toto téma.
Myslel jsem, že nelpíš jen na jednom důkazu, ale naopak bys rád těch důkazů tady viděl více. Eukleidův důkaz je troufám si říct velmi známý, ale kdo ho nezná, bude jeho krásou jistě velmi potěšen. :-)
Jinak o důkaz toho svého tvrzení jsem se zatím nepokoušel, ale asi by to šlo indukcí podle velikosti K.
"Máte úhel beta." "No to nemám."
Offline
#22 02. 11. 2011 13:06 — Editoval vanok (02. 11. 2011 21:46)
Re: najkrajsia teorema
Druhy dokaz <<MNOZINA PRVOCISIEL JE NEKONECNA>>
Este jedna varianta dokazu(podobny na prvy).
Zasa kontradikcou:
Predpokladajme ze ze mnozina vsetkych prvocisiel je konecna a nech  je najvadcie z nich.
je najvadcie z nich.
Polozme  a nech
a nech  je nejake prvocislo co deli
je nejake prvocislo co deli  .
.
Vieme ze  , a tak mame
, a tak mame  deli
deli  , a z toho mame
, a z toho mame  deli
deli 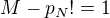 , co je kontradikcia.
, co je kontradikcia.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#23 02. 11. 2011 20:00
- check_drummer

- Příspěvky: 5446
- Reputace: 106
Re: najkrajsia teorema
vanok napsal(a):
Predpokladajme ze ze mnozina vsetkych prvocisiel je nekonecna
Překlep - konečná, že?
"Máte úhel beta." "No to nemám."
Offline
#24 02. 11. 2011 21:46
Re: najkrajsia teorema
↑ check_drummer:
dakujem za spolupracu :-)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#25 04. 11. 2011 13:04 — Editoval vanok (07. 12. 2011 12:16)
Re: najkrajsia teorema
Na dalsie dokazy vety <<MNOZINA PRVOCISIEL JE NEKONECNA>>
vam odporucam knihu od Paulo Ribenboim: The Little Book of Bigger Primes.
To je skutocne zaujimave citanie od prvej do poslednej strany
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
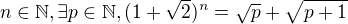
 .
.