Matematické Fórum

Saturday · 29. 11. 2007 13:50

Definice říká: Mějme množinu M, která je podmnožinou vektorového prostoru V. Průnik všech podprostorů prostoru V, které obsahují množinu M se nazývá lineárním obalem množiny M.

Není mi moc jasné, co tedy ten lineární obal vlastně je.

Vezmu to postupně na příkladu:

Vezmu například vektorový prostor 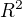$R^2$ (nad sebou samým)

Za množinu M si zvolím: M = {(1,1)}, což je podmnožina 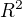$R^2$

Jak však nyní zjistím všechny podprostory prostoru V, které obsahují množinu M?

(Jeden takový podprostor W je například množina, kde pro všechny x v R platí: W= {(x,x)}, který je uzavřený na sčítání i na násobeni..)

Děkuji za odpověď

Kondr · 29. 11. 2007 22:05

Ano, v tvém případě je opravdu W= {(x,x)} lineárním obalem {(1,1)}. Možná názornější definice než "průnik všech podprostorů obsahujících prvky z M" je "množina všech lineárních kombinací všech prvků z M". Proč jsou tyto dvě definice stejné? Na jednu stranu je to jasné - každá lineární kombinace prvků z M musí ležet v každém podprostoru, který obsahuje M. Že to platí i na druhou stranu je intuitivně jasné, jestli to nenajdeš ve skriptech, tak to tu zkusím nějak napsat...

Saturday

Diky moc

Prosel jsem par skript a uz jsem to pochopil, nejjasnejsi mi prijde definice, ktera rika: $[x_1,...,x_n]=\{x;x=\sum_{j=1}^n \alpha_j x_j \text{ pro jiste skalary }\alpha_1 \in \mathrm{R}, ..., \alpha_n \in \mathrm{R}\}$ , kde $x_1, ..., x_n$ je systém vektorů z V a n>=1

poznamky:
1) $x_1, ..., x_n$ je zde ekvivalent k mnozine M (viz muj prvni prispevek)
2) Pokud jsem to pochopil spravne, tak i kdyz ta definice je ve skriptech pro 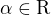$\alpha \in \mathrm{R}$ , tak obecně jde o prvek tělesa (jako "výchozí" těleso se berou reálná čísla)

Pokud se tedy vrátím ke zvolenému příkladu s M = {(1,1)} (což je systém vektorů o jednom vektoru (1,1) ),

tak z definice je vidět, že lineárním obalem je množina W= {(x,x)}, kde x nalezi R.

Lishaak · 30. 11. 2007 09:27

Ja to tak. Množině M se potom říká množina generátorů prostoru W. Ty lineární obaly jsou v lingebře důležitá věc, doporučuju zapamatovat.

dpelsiek · 01. 11. 2009 10:39

↑ Saturday:
Ahoj,
zjistil sem že nevím, co je lineární obal, a vědět to potřebuju. Ani z následujících příspěvků nejsem moc chytrý. Pomohli by jste mi prosím vyřešit následující příklad tak, abych z něj co možná nejvíc pochopil, jak se s lineárním obalem počítá? (Z příkladů často pochopím víc než z definic)

př.:
ověřte zda u=(7, 2, -2) náleží do M=Span [(1, 0, -1), (2, 1, 0), (0, 1, 2), (1, 1, 1), (5, 2, -1)]

podle definice bych asi zkusil, jestli je u lineárně závislí s některým prvkem množiny M (jestli je jeho násobkem), ale nejsem si jistý jestli by to bylo správně.

<h1>dydy</h1> · 01. 11. 2009 12:00

§je dána množina vektorů M= (1,0,0),(0,1,0),(0,0,1) . čistě náhodou to připomíná osy x,y,z "o délce 1"

Představ si lineární obal množiny M psáno <M> jako prostor, který dostaneš jako všechny lineární kombinace prvků (tedy vektorů) množiny M
psáno <M>=V
V=a(1,0,0) + b(0,1,0)+c(0,0,1) pro a,b,c z R. Skutečně. M generuje V
Současně M je báze V, protože jsou lineárně nezávislé a jsou 3 a prostor má taky dimenzi 3.
Jak jsi to pochopil od mě,?

věty z vikipedie:
Báze vektorového prostoru V je množina lineárně nezávislých vektorů, jejichž lineární obal je roven celému prostoru V. V konečně dimenzionálním prostoru dimenze n je bází každá množina obsahující n lineárně nezávislých vektorů. http://cs.wikipedia.org/wiki/Báze_(algebra)
Podmnožina M vektorového prostoru V nad tělesem T se nazývá množina generátorů prostoru V, jestliže je lineární obal této množiny roven celému prostoru V, tzn. . Říká se také, že M generuje V. http://cs.wikipedia.org/wiki/Vektorový_ … o_prostoru

lidunka.b · 01. 11. 2011 19:23

↑ Kondr: ahoj, prosimtě, můžete mi vysvětlit jak bych řekla ty závorky, které tam jsou? ty hranaté i ty kulaté?
díky

Matematické Fórum

#1 29. 11. 2007 13:50

Lineární obal - definice

#2 29. 11. 2007 22:05

Re: Lineární obal - definice

#3 29. 11. 2007 22:51 — Editoval Saturday (29. 11. 2007 23:02)

Re: Lineární obal - definice

#4 30. 11. 2007 09:27

Re: Lineární obal - definice

#5 01. 11. 2009 10:39

Re: Lineární obal - definice

#6 01. 11. 2009 12:00

Re: Lineární obal - definice

#7 01. 11. 2011 19:23

Re: Lineární obal - definice

Zápatí