Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Počet řešení soustavy lineárních rovnic - důkaz
#1 02. 11. 2011 18:07
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Počet řešení soustavy lineárních rovnic - důkaz
Ahoj zajímalo by mě, jak dokážu tvrzení, že pokud soustava lineárních rovnic má alespoň dvě řešení, pak jich má nekonečně mnoho...napadlo mě to dokázat nějak přes frobeniovu větu, ale zasekl jsem se...nějaké nápady?:)
Offline
#2 02. 11. 2011 18:15
Re: Počet řešení soustavy lineárních rovnic - důkaz
↑ Sam_Hawkins:
Ahoj,
je to velmi spatna formulacia.
Zavisi to aj na akom telese pracujes
V R^2 a v R^3 mas aj zaujimave geometricke interpretacie
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 02. 11. 2011 18:27
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Re: Počet řešení soustavy lineárních rovnic - důkaz
lze tedy povazovat za matematicky relevantni dukaz, kdyz ukazu ze (napr) pokud primky odpovidajicich rovnic maji vice nez jeden spolecny bod pak jich maji nekonecne mnoho?
A co je na te formulaci spatne?
Offline
#4 02. 11. 2011 18:33
Re: Počet řešení soustavy lineárních rovnic - důkaz
↑ Sam_Hawkins:
Nepises za akych hypotez pracujes! Treba byt presny.
Toto je jedna sdobra stopa: (o pises)
lze tedy povazovat za matematicky relevantni dukaz, kdyz ukazu ze (napr) pokud primky odpovidajicich rovnic maji vice nez jeden spolecny bod pak jich maji nekonecne mnoho?
Skus to dokonale napisat, ak by si mal taku ulohu na domacu pracu ... tak by to nebolo dostatocne.
Dobre pokracovanie
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 02. 11. 2011 18:42
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Re: Počet řešení soustavy lineárních rovnic - důkaz
ja asi porad nechapu co tomu prvnimu tvrzeni chybi...mohl by si doplnit tvrzeni o priklad hypotez o kterych mluvis?
chapu dobre ze mi radis abych rozpracoval uvahu z posledniho postu? je to spravna cesta?
Offline
#6 02. 11. 2011 18:56
Re: Počet řešení soustavy lineárních rovnic - důkaz
pisal som
Zavisi to aj na akom telese pracujes?
A neupresnil si ani to?
Pochop ze:
MATEMATIKA NIE JE NIECO OD BUKA DO BUKA, A PRETO SA TREBA TAK VYJADRIT ABY NEBOLI NEPRESNOSTI
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 02. 11. 2011 19:22
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Re: Počet řešení soustavy lineárních rovnic - důkaz
tak treba predpokladej ze je to soustava nad realnymi cisly...
a prosim te, jestli se mi snazis pomoct tak mi pomahej a nedobirej si me, jestli nechces tak nepis;)
Offline
#8 02. 11. 2011 19:35
Re: Počet řešení soustavy lineárních rovnic - důkaz
↑ Sam_Hawkins:
Ahoj kolega,
no neurazaj sa!
Ja som ti chcel len poradit... a mam vo zvyku vzdy povedat ked nieco nesedi.
Teraz si to vyjadrit dokonale.
Zo skoly vies ze linearny system ( bez parametrov) ma 0, jedno alebo nekonecne vela rieseni.
Tak ak mas dva mas nekonecno.
Srdecne Vanok
a uspesne pokracovanie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 02. 11. 2011 19:43
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Re: Počet řešení soustavy lineárních rovnic - důkaz
ano, to samozrejme vim :) Ten problem spociva v tom, jak to dokazat..:)
Offline
#10 02. 11. 2011 19:53
Re: Počet řešení soustavy lineárních rovnic - důkaz
↑ Sam_Hawkins:
no to je dosledok hodnosti matic systemu
povedzme ze sme v R^n
ak hodnost nerozsirenej matice je n; mame len jedno riesenie (vektory stlpiky tvoria bazu R^n) a vektor vytvoreny z pravej strany systemu je jedina lineaarna kombinacia.
Ak je hodnost menej ako n... pozres ci vektor vektor vytvoreny z pravej strany systemu je v lin. obale alebo nie ....
no dokonci to uz sam
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 02. 11. 2011 20:44
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Re: Počet řešení soustavy lineárních rovnic - důkaz
pockat takze ony ty vektory vytvorene ze sloupcu nerozsirene matice tvori bazi R^n jejiz linearni kombinace je vektor z pravych stran..?
a lin. obal je mnozina vsech linearnich kombinaci dane baze..?:)
Offline
#12 02. 11. 2011 20:47 — Editoval vanok (02. 11. 2011 20:47)
Re: Počet řešení soustavy lineárních rovnic - důkaz
↑ Sam_Hawkins:
Ani, iste to sa da aj inac povedat ale to je presny popis situacie
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 02. 11. 2011 20:51 — Editoval vanok (02. 11. 2011 21:21)
Re: Počet řešení soustavy lineárních rovnic - důkaz
↑ Sam_Hawkins:
Situaciu co popisujes, je ta ked hodnost zakladnej matice ma hodnost n a s to je uz vyriesene
A teraz pozeraj co sa deje ak to tak nie je:
Napriklad ak hodnost toho obalu je n-1 (precitaj si co je skryte az ked skusis sam co sa deje)
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 03. 11. 2011 12:39
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Re: Počet řešení soustavy lineárních rovnic - důkaz
nakonec jsem zvolil pomerne elegantni dukaz:
mam soustavu rovnic xA=B a jeji dve ruzna reseni x1 a x2
dokazu ze pro jakekoli t z R je i x1 + t(x1-x2) resenim:
A( x1 + t(x1-x2)) = Ax1 + t(Ax1-Ax2) = B - t(B-B) = B
prijde mi to jako korektni dukaz ne?
Offline
#15 03. 11. 2011 13:22
#16 03. 11. 2011 14:33
Re: Počet řešení soustavy lineárních rovnic - důkaz
Ahoj ↑ Rumburak:,
Ja by som povedat ze to zavisi od hodnosti matice systemu...
No nemam teraz cas, pisem z auta...
Over co je mozne v R^3 a ze matica ma hodnost 1....
Porozmyslam z papierom pro ruke a ked budem v doma odpoviem
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 03. 11. 2011 22:44 — Editoval vanok (03. 11. 2011 23:14)
Re: Počet řešení soustavy lineárních rovnic - důkaz
↑ Rumburak:
Pochopitelne co pises v formalizovanom vyjadreni je dokonale.
Ale ked pozorne precitas co pisal nas kolega ... nemame pravdu ani ty a ani ja.
vsak toto je uz same o sebe velka kontradikcia:
<<xA=B a jeji dve ruzna reseni x1 a x2...
A( x1 + t(x1-x2)) = Ax1 + t(Ax1-Ax2) = B - t(B-B) = B>>
A ked ma clovek nepresne veci povedome reaguje pri rychlom citani tak ze vidi co by chcel vidiet.
Ja som viac menej reagoval podla kontextu
" ci sa daju z dvoch rieseni vykonstruhovat vsetky ine riesenia???"
A tento post by nemal ani existovat, ak by si jeho autor zapametal a prestudoval vety o rieseniach lin. systemoch.
A co sa tyka nasich reakcii... tvojej a mojej ... sme odpovedali na otazku co nebola dobre formulovana.
Ty na to co si vysie z formalizoval... a co kazdy z nas vie...je dokonale! Ale nie je to odpoved na otazku co nie je ani dobre zformulovana
A ja som reagoval na to ze nejde a kompletne riesenie toho systemu ( ak by bol dobre napisany) a tiez to nie je na koniec dobra odpoved
... moja odpoved znamenala ze som chcel ukazat ze ak sa veznu v priklade co mi napadol dve riesenia co su v tom istom striktnom podpriestore, tak sa znich neda generovat cele generalne riesenie...
Priklad na ktory som myslel v aute je takehoto typu
1X+ 2Y+ 3Z =6
2X +4X +6Z=12
-1X-2Y-3Z =-6
Ktoreho matica je equivalentna z
1 2 3|6
0 0 0|0
0 0 0|0
a jeho riesenie sa da vyjadrit X=6 -2 Y -3Z pre kazde X, Y v R
a dve trojice riesenia
X=6; Y=0; Z=0
a
X=4; Y=1; Z=0
Nikdy ne generuju riesenia kde Z je rozne od 0
No skoda ze veta co tu vyjadrujem schematicky
Vseobecne riesenie lin. systemu = Genralne riesenie homogeneho assoiovaneho systemu + partikularne riesenie lin. sytemu
je pre vela studentov neznama....
Podla mna cely problem je v hovorovom jazyku su mozne nedorozumenia.
Aky je na to tvoj nazor?
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 04. 11. 2011 09:27
Re: Počet řešení soustavy lineárních rovnic - důkaz
↑ vanok:
Ahoj,
zatím podám jen první reakci, po podrobnějším prostudování Tvého příspěvku včetně předchozí historie se k tomu ještě vrátím.
Nedorozumění plyne, myslím, z toho, že já jsem reagoval pouze na příspěvek ↑ Sam_Hawkins:, kde autor píše
Sam_Hawkins napsal(a):
nakonec jsem zvolil pomerne elegantni dukaz:
mam soustavu rovnic xA=B a jeji dve ruzna reseni x1 a x2
dokazu ze pro jakekoli t z R je i x1 + t(x1-x2) resenim:
A( x1 + t(x1-x2)) = Ax1 + t(Ax1-Ax2) = B - t(B-B) = B
prijde mi to jako korektni dukaz ne?
Bral jsem to jako důkaz abstraktní věty, která je uvedena nějakými předpoklady. Zda v nějakém konkretním případě
jsou tyto předpoklady naplněny, to samozřejmě je duhá věc (závislá na maticích A, B) a touto stránkou jsem se nezabýval.
Offline
#20 04. 11. 2011 10:18
Re: Počet řešení soustavy lineárních rovnic - důkaz
Ahoj ↑ Rumburak:,
som rad ze dialog dokaze vysvetlit nedorozumenia
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 04. 11. 2011 11:08 — Editoval Rumburak (04. 11. 2011 11:12)
Re: Počet řešení soustavy lineárních rovnic - důkaz
↑ vanok:
Připadá mi, že jsme odpovídali každý na jinou otázku, proto se naše odpovědi lišily.
Že popisovat složitější matematické situace slovy hovorového jazyka je velký problém, to je jisté.
I během studia mi ve výkladu učitele kterékoliv matematické oblasti lépe vyhovovaly suché formule,
než nějaké "zlidšťující" slovní výklady v hovorovém jazyce, k nimž dle mých zkušeností mívali sklon
zvláště (i když ne všichni) albegraici a "strukturáři". Zároveň si ale kladu otázku, zda můj postoj
není přece jen poněkud přehnaný - někomu jinému to může vyhovovat jinak.
Offline
#22 04. 11. 2011 11:31 — Editoval vanok (04. 11. 2011 11:32)
Re: Počet řešení soustavy lineárních rovnic - důkaz
Ahoj ↑ Rumburak:,
Ja som ako ty, mozno preto ze som aj dlho pracoval v matematickej logike...
A to je nase "nestastie" ze nepresne veci nas vyvadzaju z miery.
Ale studenty nie su a zriedka budu matematici... lahko by sa nam podarilo robit ich uspojoit z nepresnostami, ale mne sa to zda necestne pre "matematiku".
A ze aj ty to poznas ak humanista hovori o literature, vsetci na neho pozeraju z obdivom, a ak ty skusis hovorit o nejakych problemoch z cistej matematiky... budes povazovany aspon za podivina ak nie za blbca
No to je zivot.
SrdecneVanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Počet řešení soustavy lineárních rovnic - důkaz

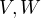 jsou lineární prostory nad společným tělesem
jsou lineární prostory nad společným tělesem  ,
,  lineární zobrazení,
lineární zobrazení,  ,
, 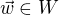 takové,
takové, 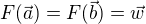 . Jestliže dále
. Jestliže dále  , kde
, kde 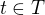 , potom
, potom .
.