Matematické Fórum

FliegenderZirkus · 03. 11. 2011 21:45

Ahoj, řeším úlohu (zadání raději píšu v originále, abych něco nepřeložil špatně):

Obtain the Euler-Lagrange equation and natural boundary conditions for the functional
$I=\iint\limits_\Omega \[ $ \frac{\partial \Phi}{\partial x}$^2+$\frac{\partial \Phi}{\partial y}$^2-4\Phi\] \text{d} x \text{d} y$

Euler-Langrangeova rovnice pro funkce dvou proměnných je
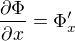$\frac{\partial F}{\partial \Phi}-\frac{\partial}{\partial x}$ \frac{\partial F}{\partial \Phi'_x} $ - \frac{\partial}{\partial y}$ \frac{\partial F}{\partial \Phi'_y} $=0$ , značím $\frac{\partial \Phi}{\partial x}=\Phi'_x$ atd.
Zde je
$F$x,y,\Phi,\frac{\partial \Phi}{\partial x}, \frac{\partial \Phi}{\partial y}$=$ \frac{\partial \Phi}{\partial x}$^2+$\frac{\partial \Phi}{\partial y}$^2-4\Phi$ ,
$\frac{\partial F}{\partial \Phi}=-4$ ,
$\frac{\partial F}{\partial \Phi'_x}=2\frac{\partial \Phi}{\partial x}$ ,
$\frac{\partial F}{\partial \Phi'_y}=2\frac{\partial \Phi}{\partial y}$ .

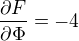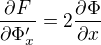Euler-Lagrangeova rovnice po dosazení a úpravě vyjde
$2+\frac{\partial^2 \Phi}{\partial x^2}+\frac{\partial^2 \Phi}{\partial y^2}=0$ .

To je snad správně, ale nevím, co se myslí okrajovými podmínkami, když žádné zadané nejsou...? Úloha souvisí s namáháním krutem. Předem děkuji za každou radu.

Pavel Brožek · 03. 11. 2011 23:54

↑ FliegenderZirkus:

Jestli jsem správně pochopil pár odkazů co jsem prošel po hledání „natural boundary conditions“ na googlu, tak se okrajové podmínky získají při integraci per partes z toho členu vyčísleného na okraji oblasti. Podrobnosti neznám.

Matematické Fórum

#1 03. 11. 2011 21:45

Eulerova-Lagrangeova rovnice

#2 03. 11. 2011 23:54

Re: Eulerova-Lagrangeova rovnice

Zápatí