Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 25. 07. 2008 21:10 — Editoval ttopi (25. 07. 2008 21:16)
Re: Výška lichoběžníku
Pokud je potřeba výšku vypočítat bez obrázku, tak bych postupopval takto.
Udělám si náčrtek lichoběžníku.
Když z obou krajních bodů horní podstavy spustíš kolmici na základnu, vznikne ti jakýsi čtverec, toho si nevšímej. Ale také ti napravo i nalevo vedle čtverce vznikly 2 trojúhelníky a ty jsou pro nás klíčové.
Oba totiž musí mít stejnou výšku. Součet základen obou trojúhelníků se musí rovnat číslu 34-12=22 - protože těch 12 patří podstavě čtverce.
Základnu levého trojúhelníku označím jako x a základnu levého trojúhelníku označím jako (22-x)
Nyní podle Pythagorovy věty musí platit, že 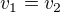 .
.
Kde 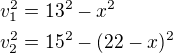
Tyto výšky dáme do rovnosi a řešíme rovnici.
Na konci nám zbyde x=9,72 periodických.
Nyní stačí dosadit buď do 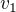 nebo do
nebo do 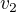 a dostaneme výšku lichoběžníku h.
a dostaneme výšku lichoběžníku h.
Tady jer pro představu, jak vzniknou ony trojúhelníky.
oo^0 = 1
Offline
#6 09. 08. 2009 20:48
Re: Výška lichoběžníku
Protože v zadání je, že celá dolní základna a je velká 34cm. Když od toho odečtu těch 12 cm jako stranu čtverce, zbyde mi 22cm.
Těchto 22 cm pak tvoří část základny vedle toho čtverce napravo + ta část nalevo.
Jelikož ani jednu neznám, tak si libovolnou určím jako x a tu druhou jako 22-x (levou jako x jsem zvolil čistě náhodou).
oo^0 = 1
Offline