Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Množina všech lineárních zobrazení (TOTO TÉMA JE VYŘEŠENÉ)
#1 05. 11. 2011 14:34
Množina všech lineárních zobrazení
Ahoj,
chtěl bych se zeptat, jak si můžu názorně představit množinu všech lineárních zobrazení. Z definice lineárního zobrazení jsem odtušil, že LZ přiřazuje vektoru vektor tak, aby platila aditivita a homogenita, tudíž jde o speciální zobrazení, které má právě tyto dvě vlastnosti (našel jsem příklady jako zrcadlení podle osy prvního a třetího kvadrantu při 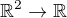 ^2, případně středová souměrnost podle počátku).
^2, případně středová souměrnost podle počátku).
Pokud vezmu tedy středovou souměrnost podle počátku v 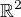 tak vektoru
tak vektoru 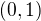 přiřadím vektor
přiřadím vektor 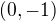 , nebo
, nebo  vektor
vektor 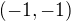 a zároveň tedy platí, že:
a zároveň tedy platí, že: který se zobrazuje na
který se zobrazuje na 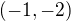 a zároveň je součet obrazů
a zároveň je součet obrazů 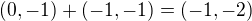 .
.
Zádrhel ale nastává, když definují množinu všech lineárních zobrazení takto:
Množinu všech lineárních zobrazení 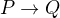 značíme
značíme 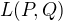 . Operace definujeme:
. Operace definujeme:

U této definice se mi nedaří vůbec představit si, co by mohla říkat, chtěl bych proto poprosit, o nějaké naťuknutí nebo příklad, jak to chápat.
Děkuji.
Offline
- (téma jako vyřešené označil(a) Sulfan)
#2 05. 11. 2011 14:48
Re: Množina všech lineárních zobrazení
Sulfan napsal(a):
Zádrhel ale nastává, když definují množinu všech lineárních zobrazení takto:
oni ale nedefinují množinu lineárních zobrazení, tu už máš. oni na ní jenom definují operace sčítání zobrazení a násobení zobrazení číslem
Offline
#5 05. 11. 2011 17:44 — Editoval Sulfan (05. 11. 2011 17:47)
Re: Množina všech lineárních zobrazení
↑ Stýv: Tudíž bych chápal, že je to hodně neformálně něco takového: 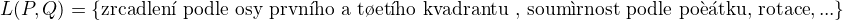
A tudíž když necháme na vektor působit dvě různá taková zobrazení (které přijdou z 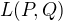 ) , tak to je totéž, jako kdybychom nechali na ten vektor působit to první, potom to druhé a následně oba vektory sečetli. A pokud budeme zobrazení násobit číslem z tělesa pak je to totéž, jako kdybychom působili tím zobrazením a nakonec ho vynásobili tím číslem, že?
) , tak to je totéž, jako kdybychom nechali na ten vektor působit to první, potom to druhé a následně oba vektory sečetli. A pokud budeme zobrazení násobit číslem z tělesa pak je to totéž, jako kdybychom působili tím zobrazením a nakonec ho vynásobili tím číslem, že?
Offline
#6 05. 11. 2011 18:00
Re: Množina všech lineárních zobrazení
↑ Sulfan:
Pre mna je tazko pochopit o co ti vlastne ide.
Tato poznamka ti mozno pomoze.
Kazda linearna applikacia sa representuje vdaka maticam ( presnosti si pozri v poznamkach z prednasok )
Studium tychto matic ti moze dat informacie co hladas
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 05. 11. 2011 18:46 — Editoval OiBobik (05. 11. 2011 19:21)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Množina všech lineárních zobrazení
↑ Sulfan:
(Asi jen zopakuju, co říkal ↑ Stýv:, ale třeba to pomůže)
Lineární zobrazení mezi dvěma vektorovými prostory je definováno za pomoci homogenity a aditivity, tak, jak to chápeš.
Množina lineárních zobrazení mezi vp P a Q je zkrátka množina 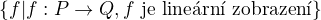 . Ve tvém případě se značí
. Ve tvém případě se značí 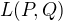 .
.
To, co máš dále definováno, jsou operace na lineárních zobrazeních pomocí operací na onom vektorovém prostoru. Tedy je tam řečeno, co je součet dvou lineárních zobrazení nebo alfa-násobek lineárního zobrazení. Dále se dá totiž ukázat, že tato lineární zobrazení sama o sobě tvoří vektorový prostor.
(Zkus si ověřit, že takto definovaný alfa-násobek libovolného lineárního zobrazení je zase lineární zobrazení, stejně tak součet lineárních zobrazení, příp. další axiomy vektorového prostoru.)
Pozn: Pokud jste ještě matice neprobírali, je ono značení lineárních zobrazení v té druhé definici (tedy té definici operací na L(P,Q)) poněkud nešťastné - 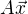 totiž značí lineární zobrazení A aplikované na vektor
totiž značí lineární zobrazení A aplikované na vektor 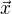 , tedy, v klasickém "funkčním" značení, by se o dalo napsat jako
, tedy, v klasickém "funkčním" značení, by se o dalo napsat jako 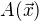 .
.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#9 05. 11. 2011 18:57
Re: Množina všech lineárních zobrazení
↑ OiBobik: Díky, začal jsem to pomalu chápat. Zkusím si dokázat vektorový prostor - měl bych tedy zkoumat - jestli je neprázdný, uzavřený na operace, na sčítání a další axiomy.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Množina všech lineárních zobrazení (TOTO TÉMA JE VYŘEŠENÉ)