Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 11. 2011 20:31
Logika
Zdravím,
mám problém s predikátovou logikou. V zadání je věta a mým úkolem je zjistit, jestli třetí věta vyplývá z prvních dvou. Mnoho takovýchto problému se dá řešit selským rozumem, ale rád bych věděl, jestli existuje řešení i pomocí matematického zápisu.
Zadání: Některé vysoké stromy jsou mrtvé. Všechno vysoké je černé. Proto vše černé je mrtvé.
Pokusil jsem se věty přepsat:
Být strom: 
Být vysoký: 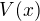
Být mrtvý: 
Být černý: 
1) Některé vysoké stromy jsou mrtvé = 
2) Všechno vysoké je černé = 
3) Vše černé je mrtvé = 

Jak to mohu upravit, abych mohl jasně říci, zda třetí věta vyplývá z prvních dvou?
Děkuji
Navštivte portál Matematika pro každého! http://maths.cz
Offline
- (téma jako vyřešené označil(a) Blujacker)
#2 06. 11. 2011 20:49
Offline
#3 06. 11. 2011 20:53 — Editoval ((:-)) (06. 11. 2011 20:57)
Re: Logika
↑ zdenek1:
Zadávateľ to možno vie - je to dosť logické...
Myslím, že by chcel vedieť, akým formálnym postupom môže prísť k správnej odpovedi.
Pripomína mi to Raymonda Smyllyana ... :-)
Ale na takúto formalizáciu nemám...
Offline
#4 06. 11. 2011 20:56
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Logika

Tohle by znamenalo, že všechno je vysoké a černé. Bude tam jiný logický operátor.
Stejně tak u .
.
---
Tady nebude to zanoření. Funkce S ti vrací 1 nebo 0, což nemůžeš předat Véčku. A taky je tu ten problém se spojkou.
Offline
#5 06. 11. 2011 21:02 — Editoval Blujacker (06. 11. 2011 21:03)
Re: Logika
↑ zdenek1:
To zrovna vím, potřebuju to formálně dokázat :-)
↑ halogan:
Ale jak to tedy mohu dokázat?
Navštivte portál Matematika pro každého! http://maths.cz
Offline
#6 06. 11. 2011 21:20
Re: Logika
↑ Blujacker:
ten první výrok bude![kopírovat do textarea $\exists x[S(x)\wedge V(x)\wedge M(x)]$](/mathtex/ee/ee79651497d445a2d23c3ac9a60067ff.gif)
důkaz zatím nemám
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#7 06. 11. 2011 21:23
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Logika
Tak ty víš, že tahle implikace neplatí.
Stačí tedy najít takové x, pro které předpoklad bude platit a závěr nikoliv.
Aby neplatil závěr, stačí najít takové x, že C(x) je pravda, ale M(x) není.
Offline
#8 06. 11. 2011 22:07
Re: Logika
↑ Blujacker:
chceme ukázat, že formule![kopírovat do textarea $\{\exists x [S(x)\wedge V(x)\wedge M(x)] \wedge \forall x[V(x)\Rightarrow C(x)]\}\Rightarrow \forall x[C(x)\Rightarrow M(x)]$](/mathtex/ed/edeffff40adaa7831f44afe39f792d76.gif)
je tautologie
podle zadání existuje prvek  tak, že
tak, že
druhá formule platí pro každé  , takže platí i pro prvek
, takže platí i pro prvek  (nutný předpoklad je, že tento prvek existuje. Pokud by neexistoval, pak je úsudek platný)
(nutný předpoklad je, že tento prvek existuje. Pokud by neexistoval, pak je úsudek platný)
a třetí formule také platí pro každé  , takže platí i pro
, takže platí i pro 
Musí tedy platit![kopírovat do textarea $\{[S(a)\wedge V(a)\wedge M(a)]\wedge[V(b)\Rightarrow C(b)]\}\Rightarrow[C(b)\Rightarrow M(b)]$](/mathtex/23/23390c7a7960d123c72e978d5fe59100.gif)
tato formule by měla být tautologie, což evidentně není, snadno se o tom přesvědčíš volbou pravdivostních hodnot:  ,
,  ,
, 
Takže úsudek neplatí
Pořádek je pro blbce, inteligent zvládá chaos!
Offline