Matematické Fórum

zuzule · 12. 11. 2011 11:05

Ahoj mám jeden příklad (k procvičení), ze kterým si moc nevím rady jak postupovat. (substituci tu řešila uživatelka zuzik1, ale dál už to počítané není), já jsem se dostala až po substituci, ale nevím jak potom dál.

Zadání: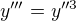
$y^{\prime\prime\prime}=y^{\prime\prime3}$

Udělala jsem substituci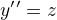
$y^{\prime}^{\prime}=z$ , $y^{\prime\prime\prime}=z^{\prime}$

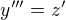
Pak když to dosadím zpátky tak mám rovnici: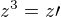
$z^3=z\prime$

napadlo mě, že bych derivaci převedla na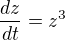
$\frac{dz}{dt}=z^3$

pak to zitegrovat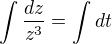
$\int\frac{dz}{z^3}=\int dt$

ale nevím, zda je můj postup správný. Mohl by mi prosím někdo poradit, co stím mám dělat a jak postupovat?

Děkuji

Alesak · 12. 11. 2011 13:22

Ahoj,

podle mě to máš správně. To dole vyřešíš jako klasickou separovatelnou rovnici. Vyšlo mi 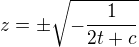$z = \pm \sqrt{-\frac{1}{2t+c}}$ . Pak akorát stačí najít podmínku pro c, aby to pod odmocninou bylo větší nebo = než 0, dosadit zpátky, a dopočítat y. Možná to pak dosadit to původní rovnice, jestli to fakt vyšlo správně.

zuzule · 12. 11. 2011 14:23

Mno a když to teda dosadím do rovnice 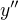$y^{\prime\prime}$ tak stím pak mám dělat co? Potřebovala bych se nějak dostat k tomuto výsledku.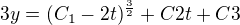
$3y=(C_1-2t)^\frac32+C2t+C3$

Já vůbec nevím jak tady postupovat a ve skriptech to máme napsaný tak jaksi divně, že se vtom nedokážu zorienovat. :-(

Alesak · 12. 11. 2011 14:40

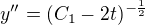Když máš $y^{\prime\prime} = (C_1-2t)^{-\frac{1}{2}}$ , tak už to stačí akorát dvakrát zintegrovat(substituce a vzoreček). Tady je ale docela lehký si ověřit správnost toho 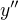$y^{\prime\prime}$ dosazením do původní rovnice, tak doporučuju udělat nejdřív to, než se pouštět do zuřivýho integrování:)

zuzule · 12. 11. 2011 15:00

Děkuju teď už to snad nějak vyřeším :-)

zuzule · 12. 11. 2011 16:53 — Editoval zuzule (12. 11. 2011 19:11)

Zkusila jsem to nějakým způsobem dopočítat, ale asi tam dělám někde nějakou blbou chybu ve znamínkách, protože se nemůžu dostat k výsledku.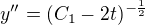

$y^{\prime\prime} = (C_1-2t)^{-\frac{1}{2}}$

Další substituce: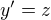
$y^\prime=z$ a $y^{\prime\prime}=z^\prime$

$(C_1-2t)^{-\frac12}=z^\prime$
$\int(C_1-2t)^{-\frac12}dt=\int dz$
$\int u^{-\frac12}\frac{du}{-2}=\int dz$
$-\frac12\frac{u^{\frac12}}{\frac12}+C_2=z$
$-(C_1-2t)^{\frac12}+C_2=z$

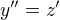
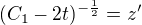
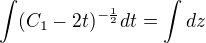
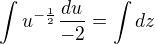
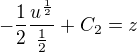
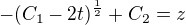
Dosadím do 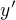$y^\prime$

$-(C_1-2t)^{\frac12}+C_2=y^\prime$

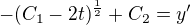
opět integruju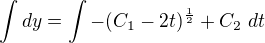
$\int dy=\int -(C_1-2t)^{\frac12}+C_2\ dt$
$y=\frac{1}{2} \frac{u^{\frac32}}{\frac32}+C_3$
$y=\frac{(C_1-2t)^{\frac32}}{3}+C_2t+C_3$

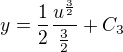
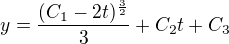
mno a toto mi vyšlo a nevím, jestli jsem tam udělala chybu nebo něco úplně špatně. Nevím jak se mám dostat ktomu výsledku, co jsem psala víš.

kaja.marik · 12. 11. 2011 19:00

$3y=(C_1-2t)^\frac32+C_2t+C_3$
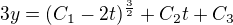
je totez co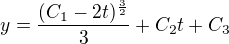
$y=\frac{(C_1-2t)^{\frac32}}{3}+C_2t+C_3$

jenom jsou konstanty C_2 a C_3 trikrat vetsi resp. mensi, podle toho, ze ktere to beru strany

zuzule · 12. 11. 2011 19:11

Aha děkuji :-)

Matematické Fórum

#1 12. 11. 2011 11:05

Diferenciální rovnice

#2 12. 11. 2011 13:22

Re: Diferenciální rovnice

#3 12. 11. 2011 14:23

Re: Diferenciální rovnice

#4 12. 11. 2011 14:40

Re: Diferenciální rovnice

#5 12. 11. 2011 15:00

Re: Diferenciální rovnice

#6 12. 11. 2011 16:53 — Editoval zuzule (12. 11. 2011 19:11)

Re: Diferenciální rovnice

#7 12. 11. 2011 19:00

Re: Diferenciální rovnice

#8 12. 11. 2011 19:11

Re: Diferenciální rovnice

Zápatí