Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#51 02. 08. 2008 01:18
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Úlohy do nepohody
↑↑ ttopi:
Pokud máš staženou ruskou klávesnici, tak je to přesně jako česká - žadné rozložení nepotřebuješ, pouze horní řádek pro taková specifická pismenka.
Nebo piš v TeX latinkou - 
A uplně nejlépe uděláš, když si poslechneš колыбельную od dobrého ruského matematika
Offline
#54 02. 08. 2008 10:02 — Editoval Marian (02. 08. 2008 10:05)
Re: Úlohy do nepohody
↑↑ jelena:
Myslim, jeleno, ze jsi spis chtela napsat "... s |q| mensi nez 1 ...".
↑↑ ttopi:
Neznam pojem klesajici rada. Prosim o vysvetleni - mozna jsem nejake zaklady teorie nekonecnych rad zaspal :-)
Offline
#56 02. 08. 2008 11:41
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Úlohy do nepohody
↑ Marian:
Určitě, přesně to jsem chtěla :-) opravím, děkuji :-)
Ted bych chtěla, abych zjistila, proč neběží jeden komunikační program, který běžet má a také se tak tvaří, že je OK - proto trochu kratím čas, než budu mít na čem zkoušet. Snad mu domluvím :-)
Offline
#57 02. 08. 2008 11:57
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Úlohy do nepohody
↑↑ ttopi:Pokud jde o ty lomené čáry: není důležité, jak ta lomená čára vypadá (kde má zlomy). Pokud se na její úseky budeme koukat jako na vektory, pak můžeme nejdřív posčítat ty, které jsou kolmé na odvěsnu a pak ty, které jsou kolmé na přeponu. Tyto dílčí součty nám vyrobí pro první lomenou čáru vektory u a v, pro druhou w a r. Je jasné, že tyto vektory nezávisí na počtu a umístění zlomů, proto můžeme předpokládat, že má každá z lomených čar jen jeden zlom. Když si takové lomené čáry nakreslíme, dostaneme dva pravoúhlé trojúhelníky podobné s ABC. Z těchto podobností
(c+b)*c/a=260,
(c+a)*c/b=78,
po úpravě
cc+cb=78a,
cc+ca=78b, navíc
cc=aa+bb (Pythagorova věta).
Jediné smysluplné řešení soustavy je c=52, a=20, b=48.
(přiznám se, to mi našla Mathematica)
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#58 02. 08. 2008 12:32
Re: Úlohy do nepohody
↑ Marian:
To nic, hlavně že já vím co to znamená a myslím, že i ostatní to pochopili :-)
↑ Kondr:
Díky za vysvětlení. Ten obrázek od jeleny je tedy špatně? Mě to přijde správně, když se na to podívám. Každá další odvěsna se vypočítá jako přepona vynásobená funkcí úhlu alfa.
oo^0 = 1
Offline
#60 02. 08. 2008 14:57
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Úlohy do nepohody
↑ ttopi: Jelenin přístup vede po dosazení za sin(alfa)=a/c, cos(alfa)=b/c na soustavu
260(c-a)=bc
78(c-b)=ac
Po dosazení stran trojúhelníku skutečně vyjde
260*4=20*52
78*32=48*52
BRKOS - matematický korespondenční seminář pro střední školy
Offline
 a
a  se zpravidla definuje jako nova posloupnost
se zpravidla definuje jako nova posloupnost  , kde
, kde 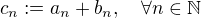 .
.