Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 15. 11. 2011 21:53
- Pavel Brožek
- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Integral e na (t na 2)
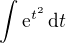
Takto? Pokud vím, tak nemá žádný hezký výsledek (nedá se vyjádřit pomocí konečného počtu elementárních funkcí).
Offline
#3 15. 11. 2011 21:55
Re: Integral e na (t na 2)
Pomocí standartních funkcí jako cos x, sin x, polynomy atd... se to nedá vyjádřit. Musela se teda udělat nová funkce, která je přesně integrál toho co chceš(krát nějaká konstanta). Jmenuje se to Error function.
Offline
#4 15. 11. 2011 21:56 Příspěvek uživatele Alesak byl skryt uživatelem Alesak.
#7 15. 11. 2011 22:35
#9 15. 11. 2011 22:39
- Pavel Brožek
- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Integral e na (t na 2)
↑ Alesak:↑ Alivendes:
Všimněte si, že v exponentu není mínus.
Offline
#10 15. 11. 2011 22:44 — Editoval ((:-)) (15. 11. 2011 22:46)
Re: Integral e na (t na 2)
↑ Alivendes:
Alivendes, čoho graf je Gaussova krivka?
Tej funkcie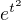 
alebo toho integrálu?
Offline
