Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prázdninová funkce (TOTO TÉMA JE VYŘEŠENÉ)
#2 01. 08. 2008 09:53
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová funkce
Bez újmy na obecnosti volím a=0. Můžu psát , protože
, protože
Pro limitu ze zadání tedy platí
 .
.
Taková funkce tedy neexistuje, nebo se pletu?
Offline
#3 01. 08. 2008 10:05 — Editoval Pavel (01. 08. 2008 10:12)
Re: Prázdninová funkce
Teď po ránu koukám, že jsem zadání mohl upřesnit (psal jsem to ve dvě v noci, kdy jsem dostal nápad :-) ). Zadání upřesním.
V literatuře se uvádí, že existuje-li  , je možné ji vypočítat jako limitu
, je možné ji vypočítat jako limitu  . Otázka je, zda existuje funkce definovaná na okolí bodu a, pro kterou předchozí limita existuje, avšak
. Otázka je, zda existuje funkce definovaná na okolí bodu a, pro kterou předchozí limita existuje, avšak  nikoli? Jednu jsem našel.
nikoli? Jednu jsem našel.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#4 01. 08. 2008 11:19 — Editoval BrozekP (01. 08. 2008 12:10)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Prázdninová funkce
Jednu bych asi měl, ale neni moc hezká:
První derivace v nule neexistuje, protože
Mohu ale vybrat dvě posloupnosti  a
a  , které s Heineho větou dávají neexistenci limity. Z neexistence první derivace v nule plyne neexistence derivace druhé. Limita ze zadání je ale rovna nule.
, které s Heineho větou dávají neexistenci limity. Z neexistence první derivace v nule plyne neexistence derivace druhé. Limita ze zadání je ale rovna nule.
Offline
#5 01. 08. 2008 11:43 — Editoval Marian (01. 08. 2008 12:35)
Re: Prázdninová funkce
Taky jsem jednu takovou funkci nasel. Definuji
kde D(x) znaci Dirichletovu funkci. Budu vysetrovat vlastnosti okoli bodu x=a:=0 (BÚNO).
(1) Plati jiste
(2) Dale vysetrim 1. derivaci funkce f(x) a ukazu, ze je rovna nule v bode x=0.
(3) Derivace ovsem neexistuje na prstencovem okoli bodu x=0. Provedu v podstate dve diskuze.
(a) Necht  je takovy bod nalezejici do prstencoveho okoli bodu x=0. Pak
je takovy bod nalezejici do prstencoveho okoli bodu x=0. Pak
Bude-li ale 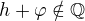 , pak je
, pak je  . Bude-li
. Bude-li  , pak je
, pak je
Ale tato limita neexistuje. Deriace zavisi na volbe cisla h a neexistuje pro  .
.
(b) Necht  je takovy bod nalezejici do prstencoveho okoli bodu x=0. Pak
je takovy bod nalezejici do prstencoveho okoli bodu x=0. Pak
Provede se stejna uvaha jako v bode (a) pro cisla  a ukaze se, ze limita zavisi na algebraicke povaze cisla h. Pro
a ukaze se, ze limita zavisi na algebraicke povaze cisla h. Pro  nebude limita existovat vubec, pro
nebude limita existovat vubec, pro  je ale
je ale  .
.
Tedy derivace neeixistuje na prstencovem okoli bodu x=0, nebude tedy existovat ani druha derivace v bode x=0.
Zaver. Funkce  splnuje Pavlovo upravene zadani.
splnuje Pavlovo upravene zadani.
Poznamka. Funkce  je o to horsi nez funkce f(x), ze nebude existovat dokonce ani limita
je o to horsi nez funkce f(x), ze nebude existovat dokonce ani limita
Offline
#7 04. 08. 2008 15:56
Re: Prázdninová funkce
↑ Marian:
Moje funkce, podle níž jsem formuloval otázku, je podobná jako Tvoje - mocnina krát Dirichlet :-) Moje původní úvaha, jak formulovat otázku, směřovala k funkci, která je v jednom bodě neomezeně diferencovatelná a všude jinde není ani spojitá, což, jak se hned ukázalo, není možné. Chtěl jsem problém směřovat na funkci
Nakonec jsem slevil ze svých požadavků, a to na druhou derivaci, a problém trochu pozměnil.
Napadla mě ještě jedna úloha:
Podobným způsobem, jako Marián ukázal, lze jednoduše vytvořit funkci diferencovatelnou v jednom bodě a nespojitou v ostatních. Otázka je:
1. Existuje funcke, která by byla diferencovatelná ve všech racionálních číslech a v iracionálních by nebyla ani spojitá?
2. Existuje funkce, která by byla diferencovatelná ve všech iracionálních číslech a v racionálních by nebyla ani spojitá?
Na dva týdny se budu muset odmlčet, takže na případné příspěvky nebudu reagovat. Zítra začnu konvergovat do Provance ve Francii.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#8 04. 08. 2008 16:06
Re: Prázdninová funkce
↑ Pavel:
Snad bude konvergence rychlá.
A pozor na mé jméno. Já jsem Marian s krátkým druhým "a". Nemám totiž české jméno, ale polské. S příjmením je to trochu jiné, to je pro změnu bulharské. Možná se budete také divit té míchanině, ale vystudoval jsem s vyznamenáním germanistiku.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Prázdninová funkce (TOTO TÉMA JE VYŘEŠENÉ)
 .
.