Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 11. 2011 16:02
- janca361

- .
- Příspěvky: 3284
Konstrukce trojúhelníku (2.35a)
Ahoj, mám příklad:
Jak mám chápat údaj 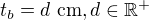 ? Mám si zvolit
? Mám si zvolit  libovolné délky?
libovolné délky?
Děkuji.
Offline
- (téma jako vyřešené označil(a) janca361)
#2 16. 11. 2011 16:04 — Editoval ((:-)) (16. 11. 2011 16:36)
Re: Konstrukce trojúhelníku (2.35a)
↑ janca361:
To d je podľa mňa parameter a treba robiť diskusiu pre jeho rozličné dĺžky vzhľadom na počet riešení úlohy.
Asi je výhodné začať od AB, naniesť uhol 60° a potom premyslieť, za akej podmienky pre dĺžku ťažnice sa dá zostrojiť stred strany b - kedy stred neexistuje, kedy je presne jeden, kedy práve dva ... (pri akej dĺžke d ťažnice).
Offline
#4 16. 11. 2011 16:39 — Editoval ((:-)) (16. 11. 2011 16:40)
Re: Konstrukce trojúhelníku (2.35a)
↑ janca361:
Myslím, že podmienky sa musia dávať pre  , teda
, teda  , ale bez
, ale bez  , lebo
, lebo  nie je dané.
nie je dané.
Offline
#5 16. 11. 2011 16:51 — Editoval janca361 (16. 11. 2011 16:58)
#6 16. 11. 2011 17:01 — Editoval ((:-)) (16. 11. 2011 17:03)
Re: Konstrukce trojúhelníku (2.35a)
↑ janca361:
Možno pomôže ...
červená 0 riešení
belasá 1 riešenie
žltá 2 riešenia
sivá 1 riešenie
a myslím, že pomôže goniometria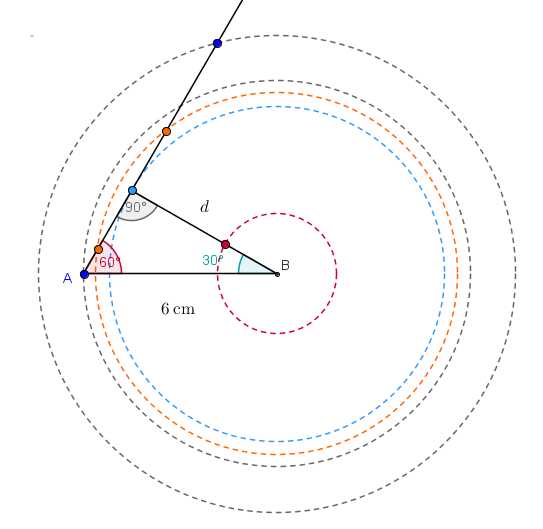
Offline
#7 16. 11. 2011 17:08
- janca361

- .
- Příspěvky: 3284
Re: Konstrukce trojúhelníku (2.35a)
janca361 napsal(a):
Úloha nebude mít řešení pro
, to je jasné.
Hloupost, 0 řešení bude pokud je 
Jak si přišla na to, že  je 90°? Je to
je 90°? Je to  ne
ne  . Nemusí nutně platit, že
. Nemusí nutně platit, že  je na
je na  kolmá, ne?
kolmá, ne?
Offline
#8 16. 11. 2011 17:18 — Editoval ((:-)) (16. 11. 2011 17:59)
Re: Konstrukce trojúhelníku (2.35a)
↑ janca361:
Teoreticky sa pokojne mohlo začať od d...
Janča - dané máš AB, BAC a d, číslo d je hocijaké kladné číslo, ibaže my nepoznáme jeho hodnotu.
Žiadne riešenie bude dovtedy, kým d bude mať takú hodnotu, že prienik k(B;d) s AX nebude existovať.
Keď meníš d (zväčšuješ ho), prvýkrát bude práve 1 riešenie vtedy, keď sa kružnica so stredom B a polomerom d polpriamky AX dotkne - odtiaľ je ten pravý uhol.
Vtedy je síce d menšie ako 6, ale predsa 1 riešenie existuje.
Od okamihu dotyku po dosiahnutie dĺžky d=6 cm existujú pri zväčšovaní hodnoty d práve dva prieniky kružnice k(B;d) s polpriamkou AX.
Akonáhle d dosiahne dĺžku 6 cm, tak už je znova iba jediný (použiteľný) prienik tejto kružnice s AX.
Otázka je, aká je horná hranica pre d... aké veľké kružidlá existujú ... :-)
Hranica existencie aspoň jedného riešenia pre dĺžku d je tá dĺžka, pre ktorú nastane dotyk.
Vtedy platí, že sa dá d vyjadriť pomocou nejakej goniometrickej funkcie, pričom v zápise využiješ dané prvky d a AB.
V diskusii skonštatuješ: ak d je od ... menšie, tak je 0 riešení, ak je d = ..., tak je práve 1 riešenie.
Ak je d väčšie ako ..., ale menšie ako ..., tak sú práve 2 riešenia.
Ak je d 6 cm alebo viac, tak je práve 1 riešenie .......
єто всё
... ale s. r. o. :-)
Offline
#9 16. 11. 2011 17:43
- janca361

- .
- Příspěvky: 3284
Re: Konstrukce trojúhelníku (2.35a)
↑ ((:-)):
Neuvědomila jsem si, že nehledám průnik kružnice s AB, ale s 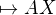 , která se přibližuje.
, která se přibližuje.
K dotyku dojde:
Pokud bude  k průniku nedojde a nebude existovat žádné řešení.
k průniku nedojde a nebude existovat žádné řešení.
Pokud  dojde k průniku ve dvou bodech a budou existovat 2 řešení.
dojde k průniku ve dvou bodech a budou existovat 2 řešení.
Ak je d väčšie ako ..., ale menšie ako ..., tak sú práve 2 riešenia.
Proč menší jako? Je tam nějaké omezení než velikost papíru a kružítka?
Offline
#10 16. 11. 2011 17:47 — Editoval ((:-)) (16. 11. 2011 17:49)
Re: Konstrukce trojúhelníku (2.35a)
↑ janca361:
Papíru a kružítka nie :-), ale ďalšia hranica je tých 6 cm, keď už znova bude iba 1 použiteľný prienik.
Vidno to na tom obrázku, ktorý je vyššie...
Neviem, či je to 100% dobre, či som tam niečo nezmršila, ale +- by to mohlo sedieť ...
Offline


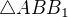 ?
? 



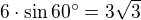
 - 0 řešení
- 0 řešení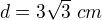 - 1 řešené
- 1 řešené - 2 řešení
- 2 řešení - 1 řešení
- 1 řešení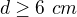 1 riešenie
1 riešenie