Matematické Fórum

zdenis · 15. 11. 2011 16:31

Zdravím, mohl by mi prosím někdo vysvětlit, jak dostanu levou stranu vzorce...nebo jaká je souvislost mezi pravou a levou. Dik
$v_{x}\frac{\partial v_{x}}{\partial x }\cdot dx=d[\frac{v^{2}_{x}}{2}]$

Andrejka3

↑ zdenis:
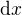Ono by se možná slušelo říct, co to $v_x$ znamená. Takhle to vypadá, že chceme provést totální derivaci nějaké funkce, která netriviálně závisí jen na jedné souřadnici (proměnné). Pak přirozeně se postupuje tak, že se spočítají příslušné parciální derivace, násobí se diferencí oné proměnné ( $\text{d}x$ ) a vše se posčítá. Ostatní parciální derivace jsou zde rovné nule. Doporučuji zjistit si, co to je totální diferenciál.

Andrejka3

↑ zdenis:
Ještě jinak. Slušné funkce jedné reálné proměnné se dají v blízkosti bodu, v němž existuje jejich derivace, aproximovat lineárně (přímkou) pomocí vztahu: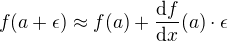
$f(a+\epsilon) \approx f(a) + \frac{\mathrm{d} f}{\mathrm{d}x }(a) \cdot \epsilon$ .
Máme-li reálnou fci více proměnných, není to už tak jednoduché. Je-li fce dostatečně slušná, dá se aproximovat lineární formou (2 dimenze plocha, 3 dimenze nadplocha atd.), které se říká totální diferenciál.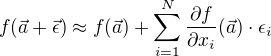
$f(\vec{a}+\vec{\epsilon}) \approx f(\vec{a}) + \sum_{i=1}^{N}\frac{\partial f}{\partial x_i}(\vec{a})\cdot \epsilon_i$ .
Tyto aproximace se používají obvykle jen v okolí bodu $\vec{a}$ a proto se často místo $\epsilon_i$ používá záhadný symbol 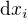$\text{d}x_i$ .

Totální diferenciál reálné fce $f$ $n$ reálných proměnných v bodě $\vec{a}$ se spočítá následovně:
$\text{d}f (\vec{a})(\vec{\epsilon})= \sum_{i=1}^{n}\frac{\partial f}{\partial x_i}(\vec{a})\cdot \epsilon_i$ .
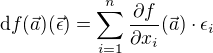Je to lineární zobrazení prostoru $\mathbb{R}^n$ do $\mathbb{R}$ . Ne každá fce má v nějakém bodě totální diferenciál. Musí být splněny jisté podmínky.

Alesak · 15. 11. 2011 20:19

Ta levá strana by mohla být externí derivací té pravé, s použitím řetízkového pravidla... ale bez dalších informací těžko říct...

zdenis · 16. 11. 2011 19:03

tady posilám konkrétní výřez ze skript..snad to nějak pomůže

Andrejka3 · 16. 11. 2011 20:37

viz můj první příspěvek + derivace složené funkce. Platí to tehdy, když $v_x$ , jakožto funkce proměnných x,y,z závisí netriviálně jen na x, tj. parciální derivace $v_x$ podle y a z je nulova.
Víc k tomu říct neumím, protože tomu více nerozumím.

Andrejka3 · 16. 11. 2011 20:39

kromě toho je mi trochu podezřelý člen druhý zleva. Neaptří tam dy místo dx?

zdenis · 17. 11. 2011 23:40

Každopádně děkuji, za příspěvky. Ještě se s tím musí trošku poprat :-/

Matematické Fórum

#1 15. 11. 2011 16:31

úprava parciální derivace

#2 15. 11. 2011 18:10 — Editoval Andrejka3 (15. 11. 2011 18:11)

Re: úprava parciální derivace

#3 15. 11. 2011 18:19 — Editoval Andrejka3 (15. 11. 2011 18:38)

Re: úprava parciální derivace

#4 15. 11. 2011 20:19

Re: úprava parciální derivace

#5 16. 11. 2011 19:03

Re: úprava parciální derivace

#6 16. 11. 2011 20:37

Re: úprava parciální derivace

#7 16. 11. 2011 20:39

Re: úprava parciální derivace

#8 17. 11. 2011 23:40

Re: úprava parciální derivace

Zápatí