Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 11. 2011 10:21
Složená relace
Zdravím, velice bych vás chtěl poprosit alespoň o nakopnutí křešení tohoto příkladu:
Mezi všemi studenty sedícími v jedné posluchárně na přednášce Úvodu do informatiky
definujeme binární relace R, S následovně:
• Student X je v relaci R se studentem Y , formálně (X, Y ) ∈ R, právě když
X sedí ve stejném sloupci jako Y
• Student X je v relaci S se studentem Y , formálně (X, Y ) ∈ S, právě když
Y sedí alespoň o dvě řady před X (tj. mezi nimi je další řada) .
Určete, které z následujících vlastností reflexivní, symetrická, antisymetrická, tranzitivní
vždy splňuje složená relace S ◦ R.
Svou odpověď musíte vždy aspoň krátce (ale přesně!) dokázat, případně uvést konkrétní
protipříklad. Odpověď bez zdůvodnění nebude honorována.
Všem, kteří mi poradí, budu moc vděčný :-)
Offline
#2 16. 11. 2011 10:48 — Editoval Andrejka3 (16. 11. 2011 16:02)
Re: Složená relace
↑ r0b1nh0:
Ahoj, nemám moc zkušeností z diskrétní matematiky, takže mé postupy nemusí být zrovna výhodné.
Nicméně zkusím poradit aspoň s reflexivitou.
Předpokládejme, že třída ma  řad a
řad a  sloupců, které očíslujeme obyčejně, podle pořadí, zleva doprava, resp. zepředu dozadu.
sloupců, které očíslujeme obyčejně, podle pořadí, zleva doprava, resp. zepředu dozadu.
Zajímá nás množina  . Tedy předpokládáme, že třída je plně obsazená (není řečeno jinak).
. Tedy předpokládáme, že třída je plně obsazená (není řečeno jinak).
Pak relace  vypadá takto:
vypadá takto:
pro  je
je  .
.
Zkus zapsat relaci  .
.
Edit: Ráda přenechám problém kolegovi. Kdybys měl ale dotaz na mě, budu se snažit odpovědět.
Edit2: hezčí znaky
What does a drowning number theorist say?
'log log log log ...'
Offline
#3 16. 11. 2011 10:53
Re: Složená relace
Stačí si uvědomit podle definice složené relace co to je, a pak už to jde samo:) Osobně si to předsavuju s šipkama. xRy je jako šipka od x k y, a složená relace je skládání šipek(jestli si to myslím blbě, tak mě opravte). Podle mě jsou všichni v relaci SR se všema, krom posledních dvou řad, kde nejsou v relaci s nikým. Za předpokladu, že je posluchárna konečná. Takže b) a d) je správně.
Offline
#4 16. 11. 2011 14:49
Re: Složená relace
↑ Andrejka3:
Díky moc, ale neměly by se první složit relace S o R a az potom posuzovat ty podminky?
Offline
#5 16. 11. 2011 14:58
Re: Složená relace
↑ r0b1nh0:
Kolega si to uvědomil hned, ale když si zapíšeš relaci S, zjistíš, že existují studenti, kteří v ní nejsou (v první složce), takže stejně tak nejsou v první složce složené relace S R. Takže reflexivita je vyloučena.
Pokud se ti nechce přemýšlet, můžeš pokračovat v mé původní odpovědi. Cesta je přímočará.
Bude to stát více psaní.
Chceš-li více přemýšlet, možná ti poradí kolega, který už reagoval.
Každopádně, za tebe to psát nebudu.
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 16. 11. 2011 15:25
Re: Složená relace
Já se v tom úplně ztrácím, ale možná se postupnými otázkami dopracuji k cíli :-D
co mi zatím došlo:
Z relace S mi vyplývá, že X nesmí sedět v posledních dvou řadách (druhá složka relace S)
a Y nesmí sedět v prvních dvou řadách (první složka relace S)
chápu to správně?
Tu reflexivitu jsem pochopil tak, že prvek nemůže být v relaci sam se sebou, protože je dané, že Y musí být před X. Asi to je špatně napsané, ale zda to chápu dobře, tak třeba relace R je reflexivní.
Ale stejně tomu vůbec nerozumím, mám pocit, že mi uniká něco důležitého, co zatím nechápu abych to mohl řešit. :(
Offline
#7 16. 11. 2011 15:41 — Editoval Andrejka3 (16. 11. 2011 15:53)
Re: Složená relace
↑ r0b1nh0:
Relace R je skutečně reflexivní, tj. ,
,
protože  . Neboli každý student (prvek M) je v relaci R sám se sebou, protože sedí ve stejném sloupci jako on sám :D (sedí ve sloupci
. Neboli každý student (prvek M) je v relaci R sám se sebou, protože sedí ve stejném sloupci jako on sám :D (sedí ve sloupci  ).
).
Relace S lze zapsat takto: .
.
Relace S není reflexivní. Je vidět, že studenti, kteří sedí v prvních dvou lavicích, nejsou v S na prvním místě. Tedy, jistě pro  , takové, že
, takové, že  ,
,
non .
.
What does a drowning number theorist say?
'log log log log ...'
Offline
#8 16. 11. 2011 15:52 — Editoval Andrejka3 (16. 11. 2011 16:03)
Re: Složená relace
↑ r0b1nh0:
Abys tomu rozumnel z hlediska formalniho, je nutne vedet, co to je slozena relace.
Budte A,B,C mnoziny. R relace mezi A,B. S relace mezi B,C.
Pak slozena relace , takže je to relace mezi A a C.
, takže je to relace mezi A a C.
Každou relaci si lze představit jako šipky. Složená relace je taky ze šipek. Šipka od a k c existuje, když je k dispozici b takové, že od a k b přejdeš šipkou první relace a od b k c šipkou druhé relace.
Edit: hezčí znaky
What does a drowning number theorist say?
'log log log log ...'
Offline
#9 16. 11. 2011 16:12 — Editoval Andrejka3 (16. 11. 2011 16:14)
Re: Složená relace
Možná to bude vyhovovat míň formálně?
Ze studentů, kteří sedí v prvních dvou lavicích nevede šipka relace S (neexistuje nikdo, kdo by seděl aspoň dvě lavice před nimi).
Kdyby složená relace byla reflexivní, tak bych se mohla od každého studenta dostat zase zpět k němu cestou přes dvě šipky, z nichž první je šipka S a druhá šipka R. Ale toto nastat nemůže, protože jsme zjistili, že ze studentů v prvních dvou lavicích nevedou šipky S.
Symetrie: Dostanem - li se od studenta x složenou relací ke studentovi y, pak se taky máme umět dostat zpět, tj. od studenta y ke studentovi x. Představ si, že jsme tedy vybrali studenta x. Kam nás šipka relace S může dostat? Ve kterém případě někam vede? Kdy nikam jít nemůžeme?
What does a drowning number theorist say?
'log log log log ...'
Offline
#10 16. 11. 2011 20:33
Re: Složená relace
↑ Andrejka3:
Na začátek bych chtěl mnohokrát poděkovat za několik pohledá jak to vysvětlit a taky za trpělivost. :-)
Pomocí těch šipek to možná chápu. Když si vezmu tu symetrii tak sipkou relace S se dostanu od prvku studenta1 ke studentovi2 sediciho o dve rady pred nim a sipkou relace R se mohu zase dostat zpet ke studentovi1, protoze sedi ve stejnem sloupci. Ale zase kdyby student1 sedel v prvnich dvou radach tak od neho nevede zadna sipka.
Pokud bych pocital se psravnosti symetrie tak mam splnenou prvni podminku antisymetrie ale nebude platit ze student1 = student2 takze to podle me neni antisymentricke
A co se tyka tranzitivity, tak zkusím takhle: sipkami relace S pojedu od studenta1 ke studentovi2 a pak od studenta2 ke studentovi3 a pak pomoci sipky relace R muzu od studenta1 ke studentovi3. Takze by mela byt tranzitivni.
Snad jsem dobře popsal jak jsem nad tim premyslel, ale se správností to bude horsi :-D
Offline
#11 16. 11. 2011 20:54 — Editoval Andrejka3 (16. 11. 2011 20:56)
Re: Složená relace
K té symetrii.
Začneme-li studentem1, jak píšeš, vede z něj spoustu šipek ke všem studentům, kteří jsou od něj aspoň dvě lavice před. Takže především musí být student1 aspoň ve třetí řadě, abychom se vůbec někam dostali.
Postupně se musíme vydat po všech šipkách relace S a prověřit všechny možnosti.
Určitě existuje šipka vedoucí do první lavice ke studentovi2 sedícím třeba ve stejném sloupci jak sedí student1. Je tedy (s1,s2)  S. Ze studenta2 vede spoustu šipek relace R. Například jedna šipka vede ze studenta2 hned zpět ke studentovi 2 díky reflexivitě relace R. Takže máme (s2,s2)
S. Ze studenta2 vede spoustu šipek relace R. Například jedna šipka vede ze studenta2 hned zpět ke studentovi 2 díky reflexivitě relace R. Takže máme (s2,s2) 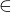 R.
R.
Proto (s1,s2)  . Jestli má být relace
. Jestli má být relace  symetrická, musí nám být umožněno se vrátit zpět. Tedy musí z něj vést šipka složené relace
symetrická, musí nám být umožněno se vrátit zpět. Tedy musí z něj vést šipka složené relace  . Tedy chci najít cestu z přestupem, první šipka je relace S a druhá relace R. Nemusí to být nutně stejná cesta zpět, jen chceme (s2,s1)
. Tedy chci najít cestu z přestupem, první šipka je relace S a druhá relace R. Nemusí to být nutně stejná cesta zpět, jen chceme (s2,s1)  .
.
Proč taková cesta neexistuje?
Ty píšeš: Když si vezmu tu symetrii tak sipkou relace S se dostanu od prvku studenta1 ke studentovi2 sediciho o dve rady pred nim a sipkou relace R se mohu zase dostat zpet ke studentovi1, protoze sedi ve stejnem sloupci. Ale zase kdyby student1 sedel v prvnich dvou radach tak od neho nevede zadna sipka.
To ale nic neřeší. Symetrická slož relace znamená: Můžeme-li se dostat z s1 do s2 pomocí S a z s2 do s3 pomocí R, pak existuje přestup s4 takový, že z s3 do s4 vede šipka S, a z s4 do s1 vede šipka R.
Může být klidně s4 = s2, ale nemusí.
What does a drowning number theorist say?
'log log log log ...'
Offline
#12 16. 11. 2011 21:01
Re: Složená relace
Nejvíce pomůže si to kreslit :)
Skládání relací je jako jízda na dovolenou s přestupem.
Transitivita (jednoduché) relace
Letecká společnost je tranzitivní, když pokud z místa A mohu letět přímo do místa B a z místa B mohu přímým spojem letět do místa C, pak taky existuje přímý spoj z A do C.
Ale nejdřív by bylo fajn dořešit tu symetrii.
What does a drowning number theorist say?
'log log log log ...'
Offline
#13 16. 11. 2011 21:36
Re: Složená relace
↑ Andrejka3:
Takze cesta tam je (s1,s2) \in S o R a musime dokazat cestu zpet (s2,s1) \in S o R. Pokud ale pri ceste tam student2 sedel v prvni lavici tak od neho nemuze vest cesta zpet ne? Tedy od studenta v prvnich dvou lavicich nevedou zadne sipky relace S.
Nebo se to bere tak, ze pri ceste tam jdeme od studenta1 o dve rady vpred ke studentovi2 a pri ceste zpet jdeme od studenta2 pres dve rady vzad ke studentovi1 ?
Asi jsem uz pochopil, ze cesta tam nemusi byt ta stejna, jako cesta zpet, dulezite je najit cesty aby dokazovali danou vlastnost.
Offline
#14 16. 11. 2011 21:42
Re: Složená relace
↑ r0b1nh0:
Výborně!
"Takze cesta tam je (s1,s2) \in S o R a musime dokazat cestu zpet (s2,s1) \in S o R. Pokud ale pri ceste tam student2 sedel v prvni lavici tak od neho nemuze vest cesta zpet ne? Tedy od studenta v prvnich dvou lavicich nevedou zadne sipky relace S."
Vzad skutečně jít nemůžeme.
Takže pokud má třída aspoň tři řady, není složená relace symetrická. Pak totiž najdem dvojici studentů takovou, že od jednoho vede šipka k druhému ale zpět ne.
Pojďme na antisymetrii.
Relace je antisymetricka, pokud plati: je -li (a,b) v relaci a též (b,a) v relaci, pak a = b.
Je naše složená relace antisymetrická?
What does a drowning number theorist say?
'log log log log ...'
Offline
#15 16. 11. 2011 22:21
Re: Složená relace
↑ Andrejka3:
Takze bych rekl ze antisymetricka neni, vychazim ze symetrie. Cesta tam je (s1,s2) S o R a cesta zpet (s2,s1)
S o R a cesta zpet (s2,s1)  S o R. Z dokazovani symetrie vime, ze (s1,s2) je v relaci ale (s2,s1) neni v relaci, tudíž neni splnena podminka pro antisymetrii.
S o R. Z dokazovani symetrie vime, ze (s1,s2) je v relaci ale (s2,s1) neni v relaci, tudíž neni splnena podminka pro antisymetrii.
Uvažuji správně?
Offline
#16 16. 11. 2011 22:35 — Editoval Andrejka3 (16. 11. 2011 22:51)
Re: Složená relace
↑ r0b1nh0:
Z toho, že relace není symetrická obecně neplyne, že je / není antisymetrická.
Porovnejme nejprve tyto dvě vlastnosti.
Symetrie. Pokud je (a,b) v relaci, pak (b,a) je v relaci.
Antisymetrie. Pokud je (a,b) v relaci a (b,a) v relaci, pak...
Takže předpoklad implikace u symetrie je o něco kratší. Když chci dokázat, že relace je antisymetrická, vypíšu si všechny dvojičky, takové, že z prvního z té dvojičky jde šipka k druhému a taky z druhého jde šipka k prvému. Jakmile mám tento seznam, podívám se, zda se mi tam vyskytla dvojička (a,b) kde 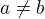 .
.
Pokud ne, je relace antisymetrická. Pokud tam taková je, není antisymetrická.
Pokud je seznam prázdný, je antisymetrická (proč? ukaž že není pravda, že relace není antisymetrická - tj. existuje prvek prázdné množiny... a je hotovo...)
Ta naše relace je ošklivá, takže nepřekvapí, pokud nebude mít žádnou z těch vlastností, které máme prověřit.
Náš cíl je: buďto
a) Napsat seznam zmíněných dvojiček ;)
b) Najít jednu dvojičku  .
.
Pomohu začátkem. Pokud má učebna nejvýše dvě řady, je naše relace prázdná a tedy antisymetrická.
Tvůj úkol:
Pokud má učebna aspoň tři řady, pak...
Co když má tři řady a jen jeden sloupec?
3 řady a více sloupců?
Vím, je to asi frustrující, ale myslím, že popocházíme.
Edit: oprava: místo antisymetrická bylo asymetrická
What does a drowning number theorist say?
'log log log log ...'
Offline
#17 16. 11. 2011 22:35
Re: Složená relace
↑ Andrejka3:
Tranzitivni
Zde uvažuji takhle, jdu od studenta1 ke studentovi2 podle relace S a od studenta2 ke studentovi2 podle relace R a dal bych musel od studenta2 ke studentovi3 podle relace S a treba od studenta3 ke studentovi3 podle relace R. Jenomze student2 uz muze sedet v prvnich dvou radach a tudiz od neho nevede zadna sipka podle relace S a nesplnime prvni podminku (cestu tam) tranzitivity.
Prosím o zkritizování :-D
Offline
#18 16. 11. 2011 22:45 — Editoval Andrejka3 (16. 11. 2011 22:47)
Re: Složená relace
↑ r0b1nh0:
Trochu máš problémy s formulací logickou, konkrétně s implikací.
Implikace se skládá ze dvou částí - z předpokladu (výrok A), a závěru (výrok B)
Mějme konkrétní výroky A,B. Výrok je pravdivý v následujícíh situacích:
je pravdivý v následujícíh situacích:
A je pravda, B je pravda
A není pravda, B je pravda
A není pravda, B není pravda.
Jediná situace, kdy implikace je nepravdivá je v případě, kdy je pravdivý předpoklad, ale nepravdivý závěr!
U tranzitivity máme přesně toto:
R je tranzitivní 
Takhle se vyhneme implikaci a stačí nám jen obecný kvantifikátor. Za ekvivalencí je...
Pro každé a,b,c z M takové, že blabla ... ":" znamená "platí, že".
Podobně antisymetrie:
R je antisymetrická 
What does a drowning number theorist say?
'log log log log ...'
Offline
#19 16. 11. 2011 22:50
Re: Složená relace
↑ Andrejka3:
Ne ne, já jsem jenom rád, že někdo má takovou trpělivost a dokáže mi pomoct.
Pochopil jsem rozdíl mezi symetrií a antisymetrií. To znamená že (s1,s2)  S o R je v relaci, máme už dokázáno a teď nevím, zda mohu tohle (s2,s1)
S o R je v relaci, máme už dokázáno a teď nevím, zda mohu tohle (s2,s1)  S o R dokázat takto: vzít si prvně studenta2 a jít ke studentovi1 o dvě řady vpřed podle relace S a pak třeba od studenta1 ke studentovi1 podle relace R. Jen ted nevím, když jsem jednou vycházel od studenta1 a podruhé od studenta2 tak za prve zda to tak muzu udelat a za druhe, zda potom teda student1 = student2?
S o R dokázat takto: vzít si prvně studenta2 a jít ke studentovi1 o dvě řady vpřed podle relace S a pak třeba od studenta1 ke studentovi1 podle relace R. Jen ted nevím, když jsem jednou vycházel od studenta1 a podruhé od studenta2 tak za prve zda to tak muzu udelat a za druhe, zda potom teda student1 = student2?
Offline
#20 16. 11. 2011 23:05
Re: Složená relace
↑ r0b1nh0:
Ať má učebna tři řady a jeden sloupec.
Jediný student, ze kterého jde šipka relace složené, je ten v té třetí řadě (Pepa). Začneme u něj. Kam můžeme jít?
Vždycky si odpověz předtím, než si to přečteš...
Šipka S nás dovede k studentovi v první lavici. Z něj chceme nastoupit na šipku relace R. Máme tři možnosti. Nastoupíme na šipku R, která vede ke studentovi v třetí řadě. Čímž, jsme absolvovali cestu po šipce složené relace. Dostali jsme se od Pepy, k Pepovi po složené šipce. Můžeme se dostat zpět, tj. od Pepy k Pepovi po složené šipce? samozřejmě, je to ta samá cesta, takže:
(Pepa, Pepa) je v relaci a obráceně taky : (Pepa, Pepa), akorát Pepa = Pepa. Takže jsme zatím nenašli dvojici, která by nesplňovala antisymetrii.
Co kdybychom nastoupili na jinou R šipku? (Tj. Pepa -> student v 1. lavici), ale ted student v prvni lavici sikpou R student v prvni nebo v druhe lavici. Tj, absolvovali jsme jednu cestu slozenou sipkou. Muzeme se dostat zpet?
Nemuzeme :)
Nas seznam vsech dvojicek, ze z prvniho te dvojicky se slozenou dostanem k druhemu a jde to i zpatky je tento:
Seznam: (Pepa, Pepa)
Zaver: Takove relace je antisymetricka.
Ať má učebna tři řady ale aspoň dva sloupce.
Co se změní? Od Pepy vede více S šipek (do jiných sloupců). Můžeme se dostat k sousedovi Pepy po pravé ruce a též naopak. Soused Pepy  Pepa a tedy tato relace je/neni...
Pepa a tedy tato relace je/neni...
Kazdopadne seznam se rozsiril.
Posledni moznost: Ucebna ma aspoň čtyři řady...
What does a drowning number theorist say?
'log log log log ...'
Offline
#21 16. 11. 2011 23:11
Re: Složená relace
↑ Andrejka3:
Jo jo, už mi to trošku dochází jak zhruba na to. Zítra se na to pořádně vrhnu a snad už to dokončím(e) celé.
Pro dnešek mnohokrát děkuji a přeji dobrou noc :-))
Offline
#22 16. 11. 2011 23:12
Re: Složená relace
↑ r0b1nh0:
Měj se, dobrou.
What does a drowning number theorist say?
'log log log log ...'
Offline
#23 16. 11. 2011 23:31 — Editoval Andrejka3 (17. 11. 2011 00:43)
Re: Složená relace
Dvě poznámky:
1) Je fajn postupovat, takhle pečlivě, jak to děláme. A taky je fajn se na to podívat globálně, když už víme, co ty vlastnosti obnášejí. Ta složená relace je představitelná (viz příspěvek Alesaka). Výsledek má rovněž okamžitě.
2) Údajně existují lidé, kteří používají opačnou konvenci pro skládání relací. :)
Zítra vstanu pozdě. Věřím, že to zvládneš sám. Dopíšu pro úplnost řešení, jen to poschovávám, ať to není hned vidět.
Takže podle kolegy vypadá naše složená relace tak, že
Reflexivita:
Symetrie: Má-li třída nejvýše
Má-li třída naopak aspoň
Antisymetrie: Pokud má třída nejvýše
Pokud má třída právě
Pokud má třída aspoň
Tranzitivita: Relace
 je
je What does a drowning number theorist say?
'log log log log ...'
Offline
#24 17. 11. 2011 16:00 — Editoval Baktor (17. 11. 2011 16:01)
Re: Složená relace
Zdravím, jako kolega řeším podobné zadání, které však zní takto:
Student A je v relaci R se studentem B , formálně (X, Y ) ∈ R, právě když
A sedí alespoň o dvě řady před B (tj. mezi nimi je další řada) .
• Student A je v relaci S se studentem B , formálně (X, Y ) ∈ S, právě když
A a B sedí ve stejné řadě a mezi nimi je alespoň jeden další student .
Pokud udělám složení relací S o R tak mi vznikne toto:
A a B nesedí ve stejné řadě a A sedí alespoň o dvě řady před B
Pokud to vezmu logicky (čili bez nějakých formálních matematických důkazů), zjistím následující:
REFLEXIVNÍ - Student A nesedí ve stejné řadě jako on sám a A sedí alespoň o dvě řady před sebou samým, čili reflexivní NENÍ
SYMETRICKÁ - pokud A sedí alespoň o dvě řady před B, tak to však neplatí opačně, že B sedí alespoň o dvě řady před A, symetrická tedy také NENÍ
TRANZITIVNÍ - pokud A je o dvě řady před B a zároveň B o dvě řady před C, tak A a C nejsou v relaci.
znázornění:
A
-
-
B
-
-
C
Poprosil bych o zhodnocení mých odpovědí a následné vysvětlení proč je to špatně (nepředpokládám, že bych to měl dobře :-D). Dále nevím jak zjistit a oddůvodnit zda-li je relace ANTISYMETRICKÁ. Byl by někdo tak hodný? Děkuju moc :-)
Offline
#25 17. 11. 2011 18:11 — Editoval Andrejka3 (17. 11. 2011 18:13)
Re: Složená relace
↑ Baktor:
Nechápu příliš odůvodnění reflexivity.
S zachová řadu, R nás posune vpřed. V posledních dvou lavicích nejsou ve složené relaci na druhém místě, tj. nevede k nim šipka. To samo o sobě stačí. Je ale jasné, že ať se vydám od libovolného studenta, s prominutím, šipkou složené relace, dostanu se dopředu, ale rozhodně mě to nevrátí na stejné místo.
Symetrie - řekla bych, že to máš ok. A,B v relaci, pak B je aspoň dvě řady před A, takže A,B nejsou v relaci.
Tranzitivita - ve tvém znázornění máš předpokládat, že dvojice A,B a dvojice B,C jsou v relaci. Pokud je relace tranzitivní, musí být A,C v relaci.
V tvém obrázku vidím: C,B B,A C,A jsou v relaci (máme dostatek sloupců).
Buď hledáme trojici, která odporuje tranzitivitě, pak stačí najít jednu. A relace není transitivní.
Nebo musíme pro všechny trojice, jež splňují předpoklad, ukázat, že splňují závěr. Pak je relace trans.
What does a drowning number theorist say?
'log log log log ...'
Offline

 množinu všech studentů. Označme
množinu všech studentů. Označme  .
.