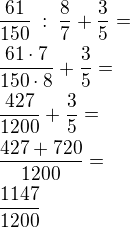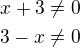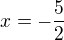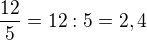Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 18. 06. 2008 20:39
Re: Zlomky
Předpokládám, že na základní škole nebudete dělat nic těžšího než:
Převod ze zlomku na číslo je jednoduchá věc. Prakticky jen vydělíš čitatele jmenovatelem. Například  . Pak může nastat těžší situace, že nepujde jednoduše krátit a pak se musí dělit vedle sebe, jak nás to učili na základce.
. Pak může nastat těžší situace, že nepujde jednoduše krátit a pak se musí dělit vedle sebe, jak nás to učili na základce.
Takže například 
To se dělá tak, že vydělíš 5:4 , což je 1 a zbytek 1. Zbytek vynásobíš x10 a máš 10 - to vydělíš znovu 4 a máš 2 a zbytek 2 - ten opět vynásobíš 10 a dostáváš 20. Vydělíš 20:4=5 a zbytek 0, tím se dostáváme k výsledku. Za 1 je desetinná čárka, protože je vidět, že čtyřka se do pětky vejde celá jen jedenkrát.
Takže  .
.
Pževádění čísla na zlomek je jednodušší.
Pokud máš třeba číslo celé, například 2, tak nemá smysl ho převádět. Ale může se, například na  ale také třeba na
ale také třeba na  , nebude-li vyžadován základní tvar zlomku.
, nebude-li vyžadován základní tvar zlomku.
Pokud je číslo desetinné, například naše 1,25 , převedeme ho na zlomek tak, že číslo vynásobíme 100 a do jmenovatele tu 100 zapíšem. Například  , což se pak upraví na základní tvar krácením. Tady se dá čitatel i jmenovatel krátit 25 a dostáváme naše původní
, což se pak upraví na základní tvar krácením. Tady se dá čitatel i jmenovatel krátit 25 a dostáváme naše původní  .
.
Stejně třeba 1,125 =  - zkrátíme čitatel i jmenovatel číslem 125 a dostaneme
- zkrátíme čitatel i jmenovatel číslem 125 a dostaneme 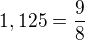 .
.
Snad ses ptala na toto, když už se s tím tak píšu :-)
oo^0 = 1
Offline
#7 02. 08. 2008 20:15 — Editoval ttopi (03. 08. 2008 00:57)
Re: Zlomky
Takhle? 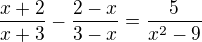
Poradím ti. Rozlož si výraz ve jmenovateli za rovnítkem, podle vzorečku  .
.
Dále budeš muset prostřední zlomek upravit tak, aby bylo stejné pořadí x a 3.Pak celou rovnici vynásob tímto jmenovatelem a zbavíš se zlomků. Pak jen upravíš co ti zbyde. Zkus to, kdyžtak zas napiš.
EDIT: Jak správně říká Chrpa, 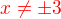
oo^0 = 1
Offline
#10 07. 08. 2008 21:53 — Editoval Marian (08. 08. 2008 00:17)
Re: Zlomky
↑ Terca a všichni ostatní:
Vím, že toto je místo, kde se zodpovídají dotazy s problematikou základní školy. Nicméně nemohu si nedovolit jednu připomínku z teorie čísel, která v jistém smyslu říká, že reálné číslo 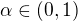 se nazývá normální, jestliže (zhruba řečeno) posloupnost cifer v jeho g-adickém rozvoji je náhodná.
se nazývá normální, jestliže (zhruba řečeno) posloupnost cifer v jeho g-adickém rozvoji je náhodná.
Tedy věta (gramatická) Potřebovala bych poradit jak se převádí zlomky na norm.čísla a naopak. se jeví velice zvláštně v duchu teorie čísel. Tento příspěvěk asi nebude mít žádnou hodnotu pro půvdního tazatele, ale přesto to zmiňuji, a? trváme na tom, aby vyjadřování bylo co možná nejpřesnějsí. Vůbec zde ale nenarážím na původní tazatelku, pouze jsem použil její slova jako médium k tomuto informativnímu sdělení.
Správně měl dotaz znít třeba takto: Potřebovala bych poradit, jak se převádí číslo ve tvaru zlomku na jeho desetinný tvar. Ale uvažme na druhou stranu, že něco takového bychom čekali jen stěží na ZŠ.
Snad primární účel mé poznámky byl ale pochopen.
edit.: Tenhle příspěvek měl ještě jeden smysl. Můj status se změnil z Pythagorás na Einstein - to se mi ale vůbec nelíbí.
Offline
#11 07. 08. 2008 23:45
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Zlomky
Využivám vzacnou přiležitost opravit sdělení ↑ Mariana :-) : - status se změnil z Pythagorás (docela chapu důvod tvého rozhorčení :-)
Nic to ovšem nemění na faktu, že je radosti číst každý Tvuj příspěvek a je potěšením splnit tvá doporučení (již neřikám "příklad", ale "zadání":-) - alespoň občas, abych to potěšení mohla patřičně užit.
Těším se na další čtení, obdivuji tvé znalosti a důslednost a přidávám malý dárek. A? se daří :-)
Offline
#12 08. 08. 2008 00:13 — Editoval Marian (08. 08. 2008 00:13)
Re: Zlomky
↑ jelena:
Jeleno, děkuji za upozornění. Ani ten Pythagorás mě moc nebavil. Mým skromným přáním je být matematikem. Zde na fóru je mnoho diskutujících, jež jsou povolanější než já, jsou to skuteční matematici. Toto fórum beru hlavně jako impuls ke svému dalšímu zdokonalení.
Děkuju za dárek!
Offline
#13 09. 08. 2008 20:05
Re: Zlomky
↑ Marian:Zdravím a blahopřeji k postupu do Einsteina , komu čest tomu čest , tvé příspěvky jsou vždy o něčem a velice ráda je pročítám vždy přinesou kvalitní osvětlení problému . S tvou poznámkou s těmi zlomky s tebou naprosto souhlasím a jen dodám , že termín : "Převod zlomku na tvar desetinného čísla ..." užívám jako učitel na ZŠ zcela běžně . Pevně věřím , že většina mých kolegů se snaží vyjadřovat také přesnými matematickými termíny . Tak tedy matematice hold a čest . :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline