Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Další izomorfní algebry (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 11. 2011 01:12 — Editoval Andrejka3 (19. 11. 2011 01:26)
Další izomorfní algebry
Ahoj.
Pro která přirozená čísla m, n jsou algebry 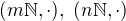 izomorfni?
izomorfni?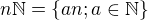
Na něco nemůžu přijít. Pomohl by mi někdo?
Co myslím, že vím:
Poslední situace je nejobecnější, co jsem asi zvládla.
Co vím, že nevím:
Edit: Zajimaji me jen m, n vetsi nez 1.
Za případné rady, opravy a připomínky předem děkuji.
A
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 19. 11. 2011 09:03 — Editoval check_drummer (19. 11. 2011 09:35)
- check_drummer

- Příspěvky: 4623
- Reputace: 99
Re: Další izomorfní algebry
↑ Andrejka3:
Ahoj.
(Skrývám chybnou úvahu)
Jak prosím vypadá tvoje bijekce f pro m=2 a n=3? Bude mít tvar
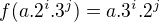 , kde a neobsahuje v rozkladu 2 ani 3?
, kde a neobsahuje v rozkladu 2 ani 3?Díky.
"Máte úhel beta." "No to nemám."
Offline
#3 19. 11. 2011 11:08 — Editoval vanok (19. 11. 2011 11:52)
Re: Další izomorfní algebry
Ahoj ↑ Andrejka3:,
Prvy problem : nerozumiem co je presne pre teba struktura Algebra
Toto?
http://cs.wikipedia.org/wiki/Algebra_(struktura)
Napis mi prosim co ten POJEM znamena v tejto peoblematike
Inac co sa tyka tvojich "pevnych bodov" zda sa mi ze nemoze existovat... az ak by islo o identitu. Napriklad, 2x3je v 6N, 2x5 je v 10N a 2 nie je v obidvoch.
Porozmyslam este o tom
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 19. 11. 2011 11:30
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
Podobně jako vanok bych si chtěl ujasnit pojmy - co znamená, že dvě algebry jsou isomorfní? Čekal bych, že algebry 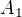 a
a 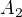 budou isomorfní, pokud existuje nějaký jejich isomorfismus. Přitom bijekce
budou isomorfní, pokud existuje nějaký jejich isomorfismus. Přitom bijekce 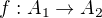 bude isomorfismus pokud pro každé dva prvky
bude isomorfismus pokud pro každé dva prvky  platí
platí  a zároveň
a zároveň  . Je to tak?
. Je to tak?
Offline
#5 19. 11. 2011 12:27
Re: Další izomorfní algebry
↑ check_drummer:
Idea konstrukce izomorfismu pro mN, nN, kde m a n jsou různá prvočísla:
číslu a z mN přiřadím číslo b, které vyrobím z a následujícím způsobem:
Napíšu rozklad a do prvočísel. Musí obsahovat člen m na kladnou mocninu. Tuto mocninu označím moc(m). Dále obsahuje mocninu u cisla n, ktera ovsem muze byt i nulova. Označím moc(n). Přehodím tyto dvě mocniny m a n. Mocnina prvocisla m v prvočíselním rozkladu čísla b je pak rovna mocnině prvoč. n u čísla a. Obdobně pro mocninu n v b.
Napíšu raději, co myslím izomorfismem, aby nedocházelo k neporozumění.
moc(děkuji za rady)
What does a drowning number theorist say?
'log log log log ...'
Offline
#6 19. 11. 2011 12:40 — Editoval Andrejka3 (19. 11. 2011 12:41)
Re: Další izomorfní algebry
↑ Pavel Brožek:
algebra (A, operace) má strukturu nosiče algebry (neprázdná množina A) a n-árních operací na nosiči.
Například (R, plus, krat, opacne cislo, nula) je algebra všech reálných čísel s operacemi binárními plus, krat, s unární operací přiřazení opačného čísla, nulární operací (konstantou) vybrání nuly. Říkáme, že tato algebra je typu (2,2,1,0). Ta čísla vyjadřují aritu příslušných operací.
Mějme A,B, dvě algebry stejného typu. (V mém problému to jsou algebry typu (2)). At f je zobrazení nosiče první algebry do nosiče druhé algebry.
Řekneme, že f je homomorfismus A,B , právě když přenáší všechny operace.
Takže pokud hvězdička je binární operací na A a plus je "odpovídající" binární operace na B, pak pro každé dva prvky a,b z A musí platit, že f(a hvězdička b) = f(a) plus f(b).
Pokud c je konstanta (nulární operace) na A a d je příslušná konstanta na B, pak musí být f(c) = d.
Analogicky pro operace jiné -arity
Řekneme, že zobrazení f mezi A, B je izomorfní, právě když je to homomorfismus A,B a zároveň bijekce A,B.
Dvě algebry jsou izomorfní, právě když existuje izomorfismus A,B.
V mém případě požaduji jen bijekci nosičů a přenášení operace krát. O žádných dalšísh strukturách není řeč (ani o sčítání, ani o uspořádání).
What does a drowning number theorist say?
'log log log log ...'
Offline
#7 19. 11. 2011 12:54
Re: Další izomorfní algebry
Ahoj ↑ Andrejka3:,
Aha to je dost nestardartne pomenovanie.
Kde a kto pouzivat takto terminologiu?
Tak v tvojom problème ide len o najdenie produktu prvocisiel co maju podobne vlasnosti.
Tak na problem m=2, n=4 tvoje struktury su isomorphe pokial nejaku ine vlasnosti ...
Ak by mali POJEM delitelnosti napr, tak ten homomohizmus by uz nefungoval...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 19. 11. 2011 12:54 — Editoval Andrejka3 (19. 11. 2011 12:55)
Re: Další izomorfní algebry
↑ Pavel Brožek:
Takže ano, přesně tak, jen předpokládáš, že obě algebry mají dvě binární operace.
Specifikovala jsem (samozřejmě, že chápu, že to nebylo zřejmé), že algebry v příkladu mají jen jednu operaci - násobení (obvyklé). Stačí tedy přenést tuto jednu operaci.
Izomorfismy zachovávají algebraické struktury - jde v podstatě jen o přejmenování prvků.
Pozorování:
Pro všechna m přirozená je mohutnost množiny m.N stejná.
Pro všechna m neexistuje konečná podmnožina mN, která generuje mN.
Pro každé m větší než, nemá mN neutrální prvek pro násobení.
Existují zvláštní prvky - takové, které nelze zapsat jako výsledek binární operace na jiných prvcích tj. cisla z mnoziny mN minus Image(operace .). Např. pro mN jsou to takové, které nejsou dělitelné m^2.
Izomorfismus musí tuto strukturu zachovat. To je jen důsledek jeho definice. Plyne aspon z toho to, že význačné prvky o nichž jsem psala se musí zobrazit na význačné prvky druhé algebry.
Třeba 2N a 3N. Tak prvky z 2N, které nedělí čtyřka (2^2) musí mít jako obraz číslo, které není dělitelné devíti (3^2).
What does a drowning number theorist say?
'log log log log ...'
Offline
#9 19. 11. 2011 12:56 — Editoval Andrejka3 (19. 11. 2011 13:00)
Re: Další izomorfní algebry
↑ vanok:
A dokážeš prosím ten izomorfismus najít? Mezi 2N a 4N? Mě se to nedaří...
Takovou definici používají pan prof. Trlifaj na MFF, obecná algebra a ...Stankovský, z jehož sbírky (zkušební verze) pochází příklady. Předmět se učí matematikové na MFF v třetím semestru asi. Poté, co absolvovali asi 2 semestry linearni algebry.
What does a drowning number theorist say?
'log log log log ...'
Offline
#10 19. 11. 2011 13:03 — Editoval Andrejka3 (19. 11. 2011 13:04)
Re: Další izomorfní algebry
↑ check_drummer:
ANO :)
To je hezky napsané to, co jsem tak složitě snažila popsat výše.
What does a drowning number theorist say?
'log log log log ...'
Offline
#11 19. 11. 2011 13:25 — Editoval vanok (19. 11. 2011 13:26)
Re: Další izomorfní algebry
Ahoj ↑ Andrejka3:,
V tej chudobej strukture : obraz 2 je 4
A jedinne co treba overit je ze obraz 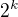 , je
, je  ...
...
Pochopitelne ak ine definicie co mas k dispozicii su tie standardne...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 19. 11. 2011 13:31
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ check_drummer:
Ten předpis by se dal zobecnit na nesoudělná čísla 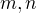 :
:  , kde a není dělitelné m ani n, nebo se pletu?
, kde a není dělitelné m ani n, nebo se pletu?
Offline
#14 19. 11. 2011 13:35
Re: Další izomorfní algebry
↑ Pavel Brožek:
Myslím, že to není přesné.
Může se stát, že když mocniny jsou různé, nemusí být obraz v množině, kam ho chceme zobrazit.
Např. 2N, 9N pak f(2) = 3
What does a drowning number theorist say?
'log log log log ...'
Offline
#15 19. 11. 2011 13:47
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
To si nemyslím, přece by bylo 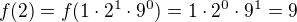 .
.
Offline
#16 19. 11. 2011 13:50 — Editoval vanok (19. 11. 2011 14:10)
Re: Další izomorfní algebry
↑ Andrejka3:,
Mas pravdu vytvoril som podstrukrury z 2N a 4N,
Nasobenie da tento homomozphismus
2 ma obraz 4 (posielam najmensi prvok na najmensi v structure 4N)
4=2x2 musi mat a potom obraz 4x4=16,(isomorfismus)
Ale potom 8 nema predobraz.
Tak tie dve struktury nie su isomorficke.
Inac v tvojom prvom prispevku si napisala, pre m, n prvocisla nN à mN su isomorficke, mozes mi napisat co to dalo pre n= 2 a m=3?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 19. 11. 2011 13:57
Re: Další izomorfní algebry
↑ Pavel Brožek:
No fakt :)
To funguje. Nádhera.
Teď se mi to ale trochu začíná motat. Myslím - Relace izomorfismus na algebrách stejného typu je ekvivalentní relací. Zatím to vypadá, že máme.
Nesoudělná čísla, ekvivalentní.
Začíná to vypadat, že bude snad vše izomorfní?
Mějme číslo přirozené. Ukažme, že mN je izomorfní 2N. Existuje přirozené číslo k, které je nesoudělné s m. Je tedy mN isomorfní kN. Požaduji navíc, aby k neobsahovalo 2. Pak jsou k a 2 nesoudělná. kN je izomorfní 2N.
Závěr:
pro každé m,n přirozené a větší než 1 platí, že mN je izomorfní nN.
Myslíte, že to je správně?
Jinak hrozně moc vám všem děkuju!
What does a drowning number theorist say?
'log log log log ...'
Offline
#18 19. 11. 2011 14:00 — Editoval Andrejka3 (19. 11. 2011 14:02)
Re: Další izomorfní algebry
↑ vanok:
No, Tvůj návrh nebyl úplný, ale pořád mi to nepřijde jako důkaz toho, že nejsou izomorfní.
Vlastně kolega nejspíš vyřešil ten problém za mně, když našel izomorfismus pro dvě nesoudělná čísla. Pak už jen stačí využít ekvivalence relace býti izomorní.
Jen by bylo fajn, kdyby ještě někdo napsal, zda souhlasí nebo ne.
Všechno si samozřejmě ještě pořádně napášu a pravda snad vyjde najevo.
What does a drowning number theorist say?
'log log log log ...'
Offline
#19 19. 11. 2011 14:06
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
To je zajímavé a docela mě to překvapuje :-). Na první pohled se to zdá správně. Můžeme tedy zkusit sestrojit isomorfismus 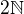 a
a  .
.
Offline
#20 19. 11. 2011 14:17 — Editoval Andrejka3 (19. 11. 2011 14:20)
Re: Další izomorfní algebry
↑ Pavel Brožek:
Tak nepostupovala jsem přesně podle návodu ale výsledek je asi stejný:
f(2^i.a) = 4^i.a
kde a neobsahuje v rozkladu 2.
Je ale zvláštní, že nás to nenapadlo hned. Když to je tak jednoduché.
Taky mě to trochu překvapilo, vzhledem k tomu, jaká cesta k tomu vedla.
Nebo že jsme nejdříve chtěli nesoudělnost.
EDIT: ano je výsledek stejný.
Díky za pomoc. Jsem nadšená. Sice to není obzvlášť zajímavá struktura, ale závěr je hezký.
What does a drowning number theorist say?
'log log log log ...'
Offline
#21 19. 11. 2011 14:26
Re: Další izomorfní algebry
↑ Andrejka3: a tvoj isomorfismus da aky predobraz prvku 8?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#22 19. 11. 2011 14:27
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ Andrejka3:
f(2^i.a) = 4^i.a
Tohle podle mě není isomorfismus. Jaké by bylo inverzní zobrazení - neodpovídala by  dvě čísla
dvě čísla  ?
?
Offline
#23 19. 11. 2011 14:30 — Editoval vanok (19. 11. 2011 14:32)
Re: Další izomorfní algebry
↑ Pavel Brožek:,
Ano presne to som konstatoval aj ja ↑ vanok:.
A aky je explicitne isomorphismus medzi napriklad 2N a 3N?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#24 19. 11. 2011 14:31 — Editoval Andrejka3 (19. 11. 2011 14:34)
Re: Další izomorfní algebry
↑ Pavel Brožek:
Obraz 16 z 2N je 4^4 z 4N, protoze 16 = 2^4
Vzor 8 z 4N: 8 = 4^1 . 2, tedy vzor = 2^1 .2 patrici do 2N.
What does a drowning number theorist say?
'log log log log ...'
Offline
#25 19. 11. 2011 14:33 — Editoval Pavel Brožek (19. 11. 2011 14:38)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Další izomorfní algebry
↑ vanok:
Máš pravdu, přehlédl jsem, že už jsi odpověděl.
↑ Andrejka3:
Ten isomorfismus 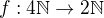 by mohl být (pokud jsem neudělal chybu)
by mohl být (pokud jsem neudělal chybu) ,
,
kde  není dělitelné dvěma ani třemi. (
není dělitelné dvěma ani třemi. ( značí dolní celou část.)
značí dolní celou část.)
Offline
- Hlavní strana
- » Zajímavé úlohy z algebry
- » Další izomorfní algebry (TOTO TÉMA JE VYŘEŠENÉ)