Matematické Fórum

Andrejka3 · 20. 11. 2011 13:32

↑↑ r0b1nh0:
Ano, jsi na dobré cestě. Tranzitivita je formulovaná dobře.
Všechno slovně je podle mě dobře.
Zkus jen zbytek formulovat matematicky.
Napíšu náš závěr pro symetrii v příspěvku č. 49, aby vše bylo pohromadě.

r0b1nh0

↑↑ Andrejka3:

Díky moc, zkusím teda tu antisymetrii a tranzitivitu.
Antisymetrie

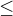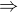1) r $\leq$ 2 $\Rightarrow$ T = $\emptyset \Rightarrow$ T je antisymetrická
2) r = 3 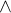$\wedge$ s = 1 $\Rightarrow (3,1),(1,3) \in M. \; ((3,1),(1,3)) \in T \;\wedge\; ((3,1),(1,3)) \in T \;\wedge\; student1=student1 (nevim jak zapsat) \Rightarrow T$ je antisymetrická
$\exists m,m' \in M : (m,m') \in T \;\wedge\; (m',m) \in T \;\wedge\; m=m'$
3) $r = 3 \wedge s \ge 1 \Rightarrow (31,11),(11,31) \in M. \; ((31,11),(11,31)) \in T \;\wedge\; ((31,12),(12,32)) \in T \;\wedge\; student1=\not student1 \Rightarrow T$ není antisymetrická

zde nevím jak zapsat případy, kdy máme více sloupců

4) $r \ge 4 \Rightarrow (3,1),(1,3) \in M. \; ((3,1),(1,4)) \in T \;\wedge\; ((4,2),(2,2)) \in T \;\wedge\; student1=\not student1 \Rightarrow T$ není antisymetrická

Tranzitivita

1) $r \leq 2 \Rightarrow T = \emptyset \Rightarrow$ T je antisymetrická
2) $r \ge 3 \Rightarrow (3,1),(1,3) \in M. \; ((3,1),(1,3)) \in T \;\wedge\; ((3,1),(1,3)) \in T \;\wedge\; (3,1),(1,3)) \in T \Rightarrow$ T je tranzitivni (pro 3 řady a jeden sloupec)
3) $r \ge 3 \Rightarrow (31,12),(12,32) \in M. \; ((31,12),(12,32)) \in T \;\wedge\; ((32,11),(11,11)) \in T \;\wedge\; (31,11),(11,11)) \in T \Rightarrow$ T je tranzitivni (pro více řad a více sloupců)

No asi to je dost špatně ale snažil jsem se :-D

Baktor · 20. 11. 2011 15:04

Andrejka3 když jsem sepisoval to co si vyřešila a když jsem narazil na tento tvůj příspěvek:
"Pokud pro každé dva A,B takové, že A je v relaci s B a B v relaci s A platí, že
A=B, pak je relace antisymetrická. V našem případě žádné A,B takové, že A je v relaci s B a současně B s A nenajdeme. Je proto antisymetrická."

Nemá tam být "Proto není antysimetrická?"

Děkuju

Andrejka3

↑ r0b1nh0:
Ad transitivita.
1) v poradku
2) Deklarujes, ze ma trida jen jeden sloupec. Pak mluvis o dvou studentech, z nichz druhy sedi v rade prvni a sloupci tretim. Asi jde o nepochopeni znaceni. Protoze kdyz se divam dal, zda se mi to nekonzistentni.
V prikladu jsou dva kartezske souciny. Prvni slouzi k tomu abychom rozlisili rady a sloupce. Druhy slouzi k tomu, abychom meli usporadane dvojice studentu.

EDIT: v příspěvku 49 jsem přidala antisymetrii.
Sice je to značení popsané jednoznačně, ale raději na příkladu:
((1,2),(3,4)) je dvojice studentů. PRvní znich sedí v první řadě a druhém sloupci.

Andrejka3 · 20. 11. 2011 17:28

↑ Baktor:
Nemá.
Bud máš problémy z definicí, nebo se ti nelíbí prázdné množiny.
Pokud je to to druhé, představ si:
Ať V je nějaká rozumna vlastnost a M PRAZDNA množina.
Mějme výrok
$\forall m \in M : V(m)$
To je pravda, protoze nasledujici neni pravda:
$\exists m \in M : \mathrm{non} V(m)$ .

r0b1nh0 · 20. 11. 2011 17:53

↑↑ Andrejka3:

Děkuji moc, je fakt že to značení jsem špatně pochopil. Jdu to sepsat a snad za to bude co nejvíce bodů.

M4R10 · 20. 11. 2011 18:28 — Editoval M4R10 (20. 11. 2011 18:30)

Zdravim, potrebuji zkontrolovat zda mam priklad dobre nebo jsem uplne mimo.

____________________________________________________________________________
Mezi všemi studenty sedícími v jedné posluchárně na přednášce Úvodu do informatiky
definujeme binární relace R, S následovně:

• Student X je v relaci R se studentem Y , formálně (X, Y ) ∈ R, právě když
X a Y nesedí ani ve stejné řadě, ani ve stejném sloupci .

• Student X je v relaci S se studentem Y , formálně (X, Y ) ∈ S, právě když
X a Y sedí hned vedle sebe v druhé řadě .

Určete, které z následujících vlastností reflexivní, symetrická, antisymetrická, tranzitivní
vždy splňuje složená relace S ◦ R.
____________________________________________________________________________

Udelal jsem si dve tabulky a pak slozenou z tech dvou:

R |a|b|c|d
a |0|1|1|1
b |1|0|0|0
c |0|0|0|0
d |0|0|0|0

S |a|b|c|d
a |0|0|0|0
b |1|1|1|1
c |0|0|0|0
d |0|0|0|0
-------------------------------
SR |a|b|c|d
a |1|1|1|1
b |0|0|0|0
c |0|0|0|0
d |0|0|0|0

Z toho mi vyslo, ze je ANTISYMETRICKA A TRANZITIVNI.

Mam aspon neco dobre? :D
Diky.

Dejwoo · 20. 11. 2011 20:30

ahojte, mam taketo zadanie :

Mezi všemi studenty sedícími v jedné posluchárně na přednášce Úvodu do informatiky
definujeme binární relace R, S následovně:
• Student X je v relaci R se studentem Y , formálně (X, Y ) ∈ R, právě když
oba sedí ve stejné řadě a Y není nalevo od X .
• Student X je v relaci S se studentem Y , formálně (X, Y ) ∈ S, právě když
X a Y nesedí ve stejné řadě, nebo nejsou hned vedle sebe .

Rad by som keby ste mi povedali ci som to spravne zlozil.

relace R sa da podla mna napisat matematicky ako (x1=y1) a (y2>x2)-cislujem z lava

relace S sa da asi napisat matematicky ako (x1 sa nerovna y1) alebo ( y2 +-1 sa nerovna x2)

a ked som to zlozil tak mi vyslo : (x1 sa nerovna y1) alebo (y2+1>x2) - to -1 odtial odpadlo pretoze podla R mohol sediet len s jednej strany

Dakujem

Andrejka3 · 20. 11. 2011 23:55

Omlouvám se, ale dál budu reagovat už jen na ty, kteří se budou snažit zapsat svou relaci v řeči formální a co nejstručněji, viz příspěvek 49. Pokud ovšem budu mít čas. Věřím, že jste schopni na základě řešení předchozích příkladů vyřešit i ten svůj.
Hodně štěstí.

Baktor · 05. 12. 2011 17:36

Tak to co jsme tu před nedávnem vyřešili, za to jsem dostal 1 bod z 16 ... neskutečně mě to naštvalo, protože jsem si celkem věřil po tom co jsme to tu rozebrali ... určitě to však nedávám za vinu Andrejka3 ... jen by mě zajímalo jak to má být tedy správně, poprosím tě jestli by si se na to moje zadání ještě nemohla zpětně kouknout a zjistit co jsme udělali špatně (tipuju, že jsem špatně složil relaci, ale těžko říct)

Děkuju

Andrejka3 · 05. 12. 2011 18:23

To mě nesmírně mrzí. Doufám, že se ozve někdo ze schopnějších / zkušenějších kolegů.

Baktor · 05. 12. 2011 18:52 — Editoval Baktor (05. 12. 2011 18:53)

Prý byla špatně složená relace a pak tedy hlavně málo důkazů proč je relace taková či maková. V tomto směru jsou podle mě na vině arogantní opravující, kteří hodnotili opravdu přísně. Nic se nestalo (myslím, že vše jsme vyřešili správně, jen to chtělo pro ty blbce více důkazů, ale to už vím pro příště :) ) ... i přesto děkuji, snad to příště dopadne lépe ;)

Matematické Fórum

#51 20. 11. 2011 13:32

Re: Složená relace

#52 20. 11. 2011 14:17 — Editoval r0b1nh0 (20. 11. 2011 14:19)

Re: Složená relace

#53 20. 11. 2011 15:04

Re: Složená relace

#54 20. 11. 2011 15:34 — Editoval Andrejka3 (20. 11. 2011 17:14)

Re: Složená relace

#55 20. 11. 2011 17:28

Re: Složená relace

#56 20. 11. 2011 17:53

Re: Složená relace

#57 20. 11. 2011 18:28 — Editoval M4R10 (20. 11. 2011 18:30)

Re: Složená relace

#58 20. 11. 2011 20:30

Re: Složená relace

#59 20. 11. 2011 23:55

Re: Složená relace

#60 05. 12. 2011 17:36

Re: Složená relace

#61 05. 12. 2011 18:23

Re: Složená relace

#62 05. 12. 2011 18:52 — Editoval Baktor (05. 12. 2011 18:53)

Re: Složená relace

Zápatí