Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 21. 11. 2011 11:09

Reshi
Příspěvky: 25
Reputace:   0 
 

MacLaurinov polynóm stupňa 8

Zdravím,

narazil som pri počítaní príkladov na tento príklad:

Určte MacLaurinov polynóm stupňa 8 pre funkciu $f(x) = ln  {|\frac{(1 - 2x + x^2)^4}{(1 + x +x^2)^2}|}$ .

Riešil som to klasicky podľa vzorca pre MacLaurinov polynóm lenže pri 5 derivácii dostávam príliš veľké čísla.

Neexistuje aj iné riešenie? Napr. možno cez nejakú substitúciu alebo podobne?

Ďakujem za odpoveď :)

Offline

 

#2 21. 11. 2011 11:29 — Editoval vanok (21. 11. 2011 11:36)

vanok
Příspěvky: 14540
Reputace:   742 
 

Re: MacLaurinov polynóm stupňa 8

Ahoj ↑ Reshi:,
To je otrocina taka metoda co si vybral.
Dam ti metodu prace...Potom to musis sam dokoncit.
Pouzi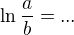
$\ln \frac ab=...$ ako aj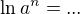
$\ln a^n=...$
Urob potom operacie co ti daju tvoj rozvoj

Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson