Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita s odmocninou (TOTO TÉMA JE VYŘEŠENÉ)
#1 15. 11. 2009 09:53
Limita s odmocninou
Dobrý den , :-)
U příkladu : "Limita s odmocninou ve zlomku" vím, že mám zlomek usměrnit. :-)
U příkladu "Limita s odmocninou " (bez zlomku) vím, že se musím zbavit odmocniny ... rozšířením .. viz odkaz :
Prosím o kontrolu postupu řešení . Výsledek mi vyšel, ale chci vědět, jestli to není jen shoda náhod.
Jde mi i o to , ve které fázi příkladu , mám dosazovat za x .. nekonečno.
Pokud se ptám hloupě , omlouvám se, jde mi o postup řešení ... polopatě :-)
Za odpovědi děkuji :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#2 15. 11. 2009 10:02
Re: Limita s odmocninou
Počkat počkat, to je celé nějaké divné, jednak  a jednak je to potřeba rozšířit chytrou jedničkou, tedy zlomkem, kde je čitatel i jmenovatel stejný (tedy (A+B)/(A+B)). Nebo neřešíš tu limitu, co je podržená?
a jednak je to potřeba rozšířit chytrou jedničkou, tedy zlomkem, kde je čitatel i jmenovatel stejný (tedy (A+B)/(A+B)). Nebo neřešíš tu limitu, co je podržená?
Vesmír má čas.
Offline
#3 15. 11. 2009 10:21
Re: Limita s odmocninou
↑ Tychi:.. Řeším tu limitu, co je podtržená... podtrhneme si zadání ...
a já se sekla ve vzorci :-(( , samozřejmě je tam chyba ..
protože : a^2-b^2=(a+b)*(a-b)
už jsem upočítaná .. to bude ono a jdu si to opravit. Děkuji za upozornění :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#7 15. 11. 2009 12:38
Re: Limita s odmocninou
Mohu poprosit o kontrolu ?
Tak jsem to nakonec vypočítala takto :
1.
Vynásobila "chytrou jedničkou" , což je vlastně usměrňování zlomku , kde si pod výraz s odmocninou napíšu jmenovatel 1
2.
Pak postupuji takto : 
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
#8 15. 11. 2009 16:39
Re: Limita s odmocninou
Teď už je to lepší, jen nevím, jestli je správné, že posíláš část k nekonečnu a další kus ještě ne. Nejdříve bys tedy měla po vytkuní x z odmocnin ho vytknout ze součtu a pak už to tak nějak rovnou vidět, že odmocniny půjdou k jedničkám, závorka půjde k dvojce, jmenovatel tedy k nekonečnu a celý zlomek tedy k nule. Tak nějak vše v jednom kroku
Vesmír má čas.
Offline
#10 15. 11. 2009 17:47
Re: Limita s odmocninou
↑ Tychi:
Ano, vidím , takže vše v jednom kroku . Děkuji :-)
↑ zdenek1:
Ano , vytýkám odmocninu z x , dám si příště pozor . Děkuji :-)
Jedna krát jedna je " tisíckrát " jedna :-)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limita s odmocninou (TOTO TÉMA JE VYŘEŠENÉ)

.jpg)
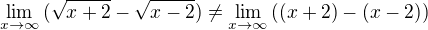


 , ne,
, ne,  . Na výsledku to ale nic neměmí.
. Na výsledku to ale nic neměmí. . Jaké by bylo pak řešení? Také
. Jaké by bylo pak řešení? Také 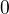 ?
?