Matematické Fórum

Spartak20 · 22. 11. 2011 18:15

Dobrý den, potřebuji vypočítat tyto 4 příklady a zároveň na jednom z nich vysvětlit postup.Je zde někdo kdo to zvládne ? Děkuji

standyk

↑ Spartak20:

e)
To $-\sin{4x}$ si rozpíš pomocou vzorca $\sin{2x}=2\sin{x}\cos{x}$
Dostaneš:
$\sin{2x}=-\sin{4x} \nl \sin{2x}=-2\sin{2x}\cos{2x} \nl -2\sin{2x}\cos{2x}-\sin{2x}=0 \nl -\sin{2x}\cdot (2\cos{2x}+1)=0$
Teraz už len riešiš tieto čiastkové rovnice:
$-\sin{2x}=0$ a $2\cos{2x}+1=0$

Spartak20 · 22. 11. 2011 19:21

↑ standyk:
děkuji a dále se to tedy řeší jak : nám to má vycházet ve stupních popř. i minutách , tento příklad měl vyjít 63 stupňů a 26 minut - jen nevím jak se k tomu výsledku dopracovat ,děkuji

standyk

↑ Spartak20:
už len dorieš tie 2 rovnice.

Môžeš použiť substitúciu $a=2x$ a teda rieš: 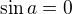$\sin{a}=0$ Z Z kalklačky alebo ztabuliek vieme že riešenie je $a=k\pi$ kde $k\in \mathbb{Z}$ Z toho teraz keď použiješ spätne substitúciu tak dostávaš: $2x=k\pi$ a teda riešenie je $x=k\frac{\pi}{2}$ kde $k\in \mathbb{Z}$

Podobne ešte musíš urobiť aj druhú čiaswtkovú rovnicu: $2\cos{2x}+1=0$

Spartak20 · 22. 11. 2011 19:44

↑ standyk:
A nemohl by jsi mi raději ukázat přesný postup (jak se dostaneš až k tomu výsledku) ? např. u toho prvního příkladu .Mě na pochopení pomáhá spíše přesná vizuální ukázka.Jinak to asi nepochopím.Díky

standyk · 22. 11. 2011 20:02

↑ Spartak20:

$2\cos{2x}+1=0$ riešiš podobne ako tú predtým. $a=2x$
$2\cos{a}+1=0 \qquad \Rightarrow \qquad \cos{a}=-\frac{1}{2}$

Kedy kosínus nadobúda hodnotu 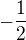$-\frac12$ Použi spätne substitúciu.
Zjednoť obidva čiastkové výsledky a máš riešenie.

Alivendes

↑ standyk:
1)

První příklad bych doporučoval toto:

$sin2x=-sin4x$
$sin2x+sin4x=0$

Vzorec:
$sin\alpha+sin\beta=2sin\frac{\alpha+\beta}{2}cos\frac{\alpha-\beta}{2}$

$sin2x+sin4x=0$
$2sin\frac{2x+4x}{2}cos\frac{2x-4x}{2}=0$
$2sin(3x)cos(-x)=0$

a)
$sin3x=0$
$x_1=\frac{k\pi}{3}$

b)
$cos(-x)=0$ cosinus je sudá funkce
$cosx=0$
$x_2=\frac{\pi}{2}+2k\pi$
$x_3=\frac{3\pi}{2}+2k\pi$

Spartak20 · 22. 11. 2011 20:35

↑ Alivendes:
asi to umíte jinak než se to učíme mi
po nás to chce učitel takto
př.

cosx+cos3x=0
cox=-cos3x
cosx=0 ---- 90 a 270 stupňů
-cos3x=0 ---- 3x ----90 a 270%
x= 30 a 90 stupňů a to je výsledek

nebo

tg2 6x+tg6x=0
tgžx(tg6x+1)=0
tg6x ---- 0 a -1

I) tg6x=0
tgy=0
y= ---- 180 a 360 stupňů

6x=y

1)6x=180
x=30 stupňů + n. 360 stupňů

2)6x=360
x=60+n.360 stupňů

II)

tg6x=-1

1)
6x=135 stupňů
x=22 stupňů a 30 minut + n.360

2)
6x=315 stupňů
x=52stupňů a 30 minut + n.360

Nejhorší natom je, že je učitel zvyklý učit z výšky a tak neumí pořádně učit na střední.Neumí nám to dobře vysvětlit.... a ty vzorce na které jste upozorňoval vy, tak podle tich to dělat stejně nemůžu ..musíme se vždy držet toho postupu co nám dá on.Pokud tedy přijdete na nějaký jednoduchý systém v těch 4 příkladech ,budu ráda,děkuji

Alivendes

To co jsem napsal je součtový vzorec pro goniometrické funkce, na to není co umět ....

A navíc to co píšeš je špatně.
$tg6x=0$
$6x=k\pi$
$x=\frac{k\pi}{6}$

$tg6x=-1$
$6x=\frac{3k\pi}{4}$
$x=\frac{3k\pi}{24}$

.........

Spartak20

↑ Alivendes:
no nic, tohle nikam nevede(my vzorce s k a pí nepoužíváme)
nevím co je na tom špatně ,ale diktoval nám to včera sám učitel
zítra si radši dojdu na doučování k jinému učitely(člověku), který to pro změnu umí i vysvětlit
i tak Vám děkuji a nashledanou

Alivendes

1) Tangens nemá periodu 360 stupňů ale 180 stupňů

2) když máš příklad

$tg6x=0$
$6x=n.180°$
$x=\frac{n.180°}{6}=n.30°$

Musíš dělit i periodu.

Matematické Fórum

#1 22. 11. 2011 18:15

Goniometrické rovnice

#2 22. 11. 2011 19:08 — Editoval standyk (22. 11. 2011 19:08)

Re: Goniometrické rovnice

#3 22. 11. 2011 19:21

Re: Goniometrické rovnice

#4 22. 11. 2011 19:36 — Editoval standyk (22. 11. 2011 19:37)

Re: Goniometrické rovnice

#5 22. 11. 2011 19:44

Re: Goniometrické rovnice

#6 22. 11. 2011 20:02

Re: Goniometrické rovnice

#7 22. 11. 2011 20:14 — Editoval Alivendes (22. 11. 2011 21:08)

Re: Goniometrické rovnice

#8 22. 11. 2011 20:35

Re: Goniometrické rovnice

#9 22. 11. 2011 20:43 — Editoval Alivendes (22. 11. 2011 20:46)

Re: Goniometrické rovnice

#10 22. 11. 2011 20:59 — Editoval Spartak20 (22. 11. 2011 21:02)

Re: Goniometrické rovnice

#11 22. 11. 2011 21:04 — Editoval Alivendes (22. 11. 2011 21:07)

Re: Goniometrické rovnice

Zápatí