Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#26 23. 11. 2011 20:09
Re: Ruleta - pravděpodobnost
↑↑ radekm:
ano, pokud si nedam cil, ktery jsme si stanovili na zdvojnasobeni vkladu - cilize dosahnout 2048Kc na konte
Offline
#27 23. 11. 2011 20:44 — Editoval Pavel Brožek (23. 11. 2011 20:48)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Ruleta - pravděpodobnost
↑↑ radekm:
Pravda, neřekl jsem jasně čeho pravděpodobnost. Hra má dva možné výsledky (když neuvažuji nekonečnou hru, která má ale nulovou pravděpodobnost) – buď dosáhnu částky alespoň 2048 nebo zbankrotuji. Měl jsem na mysli pravděpodobnost jedné z těchto možností.
Měl jsem v programu chybu, takže ten předchozí výsledek neplatí. Snad už správný výpočet mi teď běží mnohem pomaleji. Prošel jsem 10000 her, částky alespoň 2048 jsem dosáhl v 4992 hrách a zbankrotoval jsem v 5008 hrách. (Možnost, že padne nula jsem opět neuvažoval.)
Offline
#28 23. 11. 2011 20:52
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Ruleta - pravděpodobnost
Pokud uvažuji, že pravděpodobnost výhry v jednom hodu je 18/37, pak jsem z 10000 her zdvojnásobil vklad v 3804 případech a zbankrotoval v 6196 případech.
Offline
#29 23. 11. 2011 21:26
Re: Ruleta - pravděpodobnost
zajimavy
kdyz to ale vezmu z lidskeho hlediska, nemam tolik pokusu, ma jen jeden
procentualni vyuctovani toho, ze o vse prijdu behem 1024 uspesnych pokusu - neuspesne nepocitam
je tedy vice nez 50%
50% sance ze se stane ze 10x padne jina barva nez sazim je vcelku dost,
pak se tedy ptam
plati to i pro moznost, ze si naskudlim vic penez a skusim jit na 15 spatnych - pak mam, jak jsem uvedl 65.503kc
aby mi to vse 16 pokus vratil
plati to i tak? nebo se moje sance zvedne
Offline
#30 23. 11. 2011 23:24 — Editoval Pavel Brožek (27. 11. 2011 21:10)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Ruleta - pravděpodobnost
S pravděpodobností výhry 18/37 v jednom hodu jsem to nechal napočítat pro různé výchozí a konečné stavy:
Code:
začátek cíl výher bankrotů
1 2 4854 5146
2 4 4779 5221
4 8 4681 5319
8 16 4613 5387
16 32 4528 5472
32 64 4401 5599
64 128 4191 5809
128 256 4120 5880
256 512 4045 5955
512 1024 3960 6040
1024 2048 3804 6196
2048 4096 3753 6247
4096 8192 3562 6438
8192 16384 3440 6560Je tedy jasně vidět, že jak částky narůstají, tak přestože se vždy snažíme vklad zdvojnásobit, pravděpodobnost zdvojnásobení klesá. Je ovšem otázka, jestli k nule nebo nějaké konstantě…
Edit: Doplněny hodnoty pro začátek 1 až 64.
Offline
#31 23. 11. 2011 23:44
#32 24. 11. 2011 00:04
Re: Ruleta - pravděpodobnost
↑ Pavel Brožek:
je tedy zrejme, ze cim vic hci vydelat, tim hur to jde
co kdyz ale budu mit jasny cil, napriklad nahrat 2000Kc, a vezmu si ktomu napr 8192Kc abych ustal nekolik proher v rade - bude riziko bankrotu adekvatni mozne vyhre?
Offline
#33 27. 11. 2011 17:12 — Editoval FailED (27. 11. 2011 17:17)
Re: Ruleta - pravděpodobnost
↑ Pavel Brožek:
Zdravím,
bankrot znamená "došly žetony" nebo "nelze pokračovat v martingale"?
Edit: A nebo jsi to dělal tak, že když nezbylo dost žetonů na jednu sázku, tak si sázel všechno tak dlouho, nežs nenasázel dost?
Offline
#34 27. 11. 2011 18:49
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Ruleta - pravděpodobnost
↑ FailED:
Ahoj, nejsem si jistý, jestli rozumím dobře otázce. Bankrot pro mě znamená, že nemám žetony. Takže kdybych např. vsadil 4, prohrál a zbyly mi 3 žetony, tak nekončím, ale vsadím ty tři žetony. Pokud je prohraju, zbankrotoval jsem. Pokud vyhraju, tak mám 6 žetonů a zase začínám na sázce 1 (bez ohledu na to, že jsem předtím nedosáhl zisku 1 žeton).
Offline
#35 27. 11. 2011 19:42
Re: Ruleta - pravděpodobnost
↑ Pavel Brožek:
Aha, takže ještě jinak :)
Zkoušel jsem to odhadovat a povedlo se jen pro ten nejjednodušší případ - že při nedostatku žetonů na sázku skončíme, pravděpodobnosti pro ten tvůj způsob z toho možná půjdou dopočítat.
Napíšu svůj postup, možná mi tam najdete chybu nebo to třeba tady někdo dopočítá nebo se k tomu zkusím vrátit později:
Pro případ, že skončíme, pokud nemáme dost žetonů na sázku:
máme 2^n-1 žetonů, cíl je 2^(n+1)-1, potřebujeme vyhrát 2^n krát, rozdělíme si hru na fáze, ve kterých nejdřív prohráváme a nakonec vyhrajeme, když prohrajeme n* za sebou, končíme.
Ve fázi prohrajeme 0-krát s pravděpodobností p, jednou s pravděpodobností (1-p)*p, k-krát s pstí (1-p)^k*p, aspoň k-krát s pstí (1-p)^k, méně než n-krát s pstí 1-(1-p)^n.
Pravděpodobnost, že v žádné fázi neprohrajeme aspoň n* je (1-(1-p)^n)^(2^n).
Dále můžeme spočítat, jaká je pst toho, že prohrajeme v k-té fázi, vsadíme zbylé žetony a vyhrajeme. Potom můžeme spustit výpočet nanovo pro vhodné parametry.
Offline
#36 27. 11. 2011 20:57
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Ruleta - pravděpodobnost
↑ FailED:
Dá se snadno spočítat, že limita tvé pravděpodobnosti pro 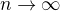 je pro
je pro  rovna 1, pro
rovna 1, pro 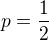 je rovna
je rovna  a pro
a pro  je rovna 0.
je rovna 0.
Dále v tomto příspěvku předpokládám  .
.
Dal jsem tvé teoretické výsledky a mé numerické do jednoho grafu:
Na vodorovné ose je n, na svislé pravděpodobnost, že počáteční vklad zvětšíme o 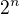 (v mém případě tedy zdvojnásobíme). Mé modré výsledky jsou pro počáteční vklad
(v mém případě tedy zdvojnásobíme). Mé modré výsledky jsou pro počáteční vklad 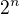 (oproti tvým červeným s
(oproti tvým červeným s 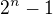 ), takže to není úplně to samé, ale myslím, že rozdíl je zanedbatelný (předpokládám, že tvůj způsob výpočtu, kde např. pro n=1 chceme vklad vlastně ztrojnásobit, může za to ohnutí dolu pro malá n).
), takže to není úplně to samé, ale myslím, že rozdíl je zanedbatelný (předpokládám, že tvůj způsob výpočtu, kde např. pro n=1 chceme vklad vlastně ztrojnásobit, může za to ohnutí dolu pro malá n).
Je tedy vidět, že rozdíl mezi tvým a mým způsobem není pro rozumné hodnoty n zanedbatelný.
Offline
#37 19. 01. 2012 17:46
Re: Ruleta - pravděpodobnost
nazdar lidi. já vás pořád nějak nechápu. říkáte, že pravděpodobnost barvy je pořád stejná protože ruleta nemá paměť a pak počítáte pravděpodobnost šesti po sobě stejných barev jako 18/37 to celé na šestou, což je 1,32 %. to se mi vůbec nezdá. vždyť šest stejných barev padne dost často. já sem hrál na 14 možných sázek po sobě a zbankrotoval jsem. podle tohoto výpočtu 18/37 a to celé na 14 mi vychází 0,0042 %. to už přece ani není žádná pravděpodobnost ale úplně mizivá hodnota. tak já teď nevím co si myslet.....
Offline
#38 19. 01. 2012 17:51 — Editoval Pavel Brožek (19. 01. 2012 17:55)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Ruleta - pravděpodobnost
↑ maxboo:
Téma je dlouhé a starší, takže si nepamatuji podrobnosti, co jsme tu řešili, a nechce se mi ho pročítat. Můžeš být konkrétnější v tom, co znamená „já sem hrál na 14 možných sázek po sobě a zbankrotoval jsem.“? Pravděpodobnost, že „čtrnáctkrát po sobě si vsadíš na nějakou barvu a pokaždé prohraješ“, je skutečně (18/37)^14. Tento „pokus“ (tj. těch 14 hodů) samozřejmě nesmíš opakovat – pravděpodobnost, že toto nastane alespoň jednou při více „pokusech“ samozřejmě roste. Nevím ale, jestli je to to, na co se ptáš.
Offline
#39 19. 01. 2012 19:18
Re: Ruleta - pravděpodobnost
↑ Pavel Brožek:
myslím tím to že sem začal sázek na černou a po každé prohře jsem zdvojnásobil sázku a po čtrnácti červených sem už neměl co sázet. prostě přišla řada 14 červených po sobě. nezdá se mi že má šance na výhru byla 1 - (18/37)na 14 což je 99,9958. nevím jestli ty výpočty chápu dobře. opakovat sem nic nechtěl ale když to prostě přijde tak to přijde :-)
Offline
#40 19. 01. 2012 21:03 — Editoval Pavel Brožek (19. 01. 2012 21:31)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Ruleta - pravděpodobnost
↑ maxboo:
Tak to jsi měl opravdu velké „štěstí“, že čtrnáctkrát po sobě nepadla černá hned po tom, co jsi začal hrát. Šance, že se to stane, byla opravdu malá. Zkus si takových čtrnáct hodů zopakovat třeba 1000000 krát (tj. celkem 14000000 hodů). Uvidíš, že jen asi v 89 případech ti 14 krát za sebou nepadne černá.
Offline
#41 19. 01. 2012 21:28
Re: Ruleta - pravděpodobnost
↑ Pavel Brožek:
to jsem teda fakt šťastlivec. a ještě dotaz....když tady říkáte že pravděpodobnost některé barvy je pořád stejná protože ruleta nemá paměť, jak to že se teda dá spočítat pravděpodobnost např. šesti po sobě jdoucích stejných barev? nebo teda v mém případě 14 :-) podle toho co tady zaznělo by i po 14 měla být stejná pravděpodobnost jako poprvé né?
Offline
#42 19. 01. 2012 21:32 — Editoval Pavel Brožek (19. 01. 2012 21:33)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Ruleta - pravděpodobnost
Ano, po 14 hodech (ať v nich padlo cokoliv) je v dalším hodu pravděpodobnost, že padne černá, stále 18/37.
(V předchozím příspěvku jsem opravil číslo z 42 na 89, špatně jsem počítal – místo 19/37 jsem použil 18/37.)
Offline
#43 28. 01. 2012 11:19 — Editoval dosman (28. 01. 2012 11:57)
Re: Ruleta - pravděpodobnost
Ahoj všem,
vidím že jste tady opravdu hlavy. Tak k mému dotazu. Martingale ale trosku jinak. Jaká je šance že z 20ti hodů po sobě spadne 4x a více stejná barva?
V praxi... Mám 1000 korun, rozhodnu se sázet jen na červenou. Sázky budou 50 150 300 500 (v pripade ze neuspeju, jinak vzdy kdyz vyhraju, dalsi sazka je zase 50). a teď otazka. je matematicka sance 100% a vyšší že za tech 20 hodů prohraju, tzn. spadne černá 4x a více x za sebou, nebo není (50x20 je vklad)? pokud ne, při dostatečně dlouhém opakování bych totiž měl jistou šanci na výhru. děkuji :)
Edit: nezapominejme na nulu...
Offline
#44 28. 01. 2012 11:24 — Editoval dosman (28. 01. 2012 11:25)
Re: Ruleta - pravděpodobnost
maxboo napsal(a):
↑ Pavel Brožek:
to jsem teda fakt šťastlivec. a ještě dotaz....když tady říkáte že pravděpodobnost některé barvy je pořád stejná protože ruleta nemá paměť, jak to že se teda dá spočítat pravděpodobnost např. šesti po sobě jdoucích stejných barev? nebo teda v mém případě 14 :-) podle toho co tady zaznělo by i po 14 měla být stejná pravděpodobnost jako poprvé né?
Wikipedie
Opakujme náhodný pokus N-krát, přičemž předpokládejme, že výskyt náhodného jevu A pozorujeme v K případech. Číslo K se nazývá četností jevu A. Poměr K/N se pak označuje jako poměrná či relativní četnost jevu A. Jestliže se s rostoucím N, tedy se zvyšováním počtu opakování pokusu, relativní četnost K/N blíží nějakému číslu, pak toto číslo můžeme považovat za pravděpodobnost daného jevu.
Offline
#45 09. 07. 2012 00:04 — Editoval krutak (09. 07. 2012 00:07)
Re: Ruleta - pravděpodobnost
Cus, Uz se na to asi ptal dosman, ale nak sem nepochopil jak to mam spocitat... Jak spocitam pravdepodobnost, ze treba pri 150 hodech mi alespon 1x padne 6x po sobe cervena? (=pravdepodobnost, ze behem 150 hodu zkrachuju kdyz hraju martingale a mam jen na 6 hodu)
Offline
#46 18. 07. 2012 00:00 — Editoval syn matematika (18. 07. 2012 00:20) Příspěvek uživatele syn matematika byl skryt uživatelem Lukee. Důvod: Příspěvek nedává smysl
#47 22. 08. 2017 10:50
Re: Ruleta - pravděpodobnost
V problémech jako je barva na ruletě nebo házení mincí se snadno zamění dvě věci. Pravděpodobnost žádané barvy při každém točení je pořád stejná. Pravděpodobnost, že udělám šňůru třeba pěti stejných za sebou je pak mnohem menší, ale je to pravděpodobnost celé serie. Každé kolo v ní mělo stejnou pravděpodobnost.
Proto když dlouho nepadla červená, tak není větší šance, že padne. Byla malá pravděpodobnost, celé té šňůry, která do toho bodu vedla, ale každý krok, který ji tvořil, měl stejnou pravděpodobnost a bude to tak i s dalším krokem, který na ni naváže. Buďto šňůru přeruší, nebo ji prodlouží, ale pravděpodobnost je pořád stejná.
Jinak jestli si chcete ověřit různé strategie, tak neváhejte vyrazit online. :) Na ruletě klidně můžete vydělat, jenom ne cíleně a ani ne dlouhodobě. Hrajte pro zábavu ze hry a vzrušení z rizika, ne pro to, abyste vydělávali peníze. :)
Offline
#48 07. 06. 2021 20:30
Re: Ruleta - pravděpodobnost
Předchozí čísla ani barvy nemají žádný vliv na následující kolo, pokud neni ruleta žádným spôsoom ovlivněna. Klidně se může stát, že i 10x po sobě padne červená nebo černá. Dobře to je rozepsáno iv tomto článku, jako celá tato mechanika funguje. Existuje i taktika ve které sázíš stále na tutéž barvu a vždy zdvojnásobíš sázku pokud prohraješ a na konci by si měl "určitě vyhrát", ale v tomto případě se může stát, že mnohdy za sebou padne stejná barva a spíše ti dojdou peníze, čili je to vše o štestí v dlouhodobém měřítku nelze vytvořit nějaká taktika na základě toho, co padlo před tím.
Offline
