Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 27. 11. 2011 00:08
Derivace funkce v bodě
Dobrý den, mám problém s úlohou zaměřenou na derivaci funkce v bodě. Na základě definice derivace mám určit derivaci funkce f v bodě a > 0.
Zadání: 
Můj postup:


a dále se prostě nedostanu, mám tam stále nějaké chyby.
ještě bychto mohl upravit:
Teď už fakt nevím, jak dál :( Prosím o radu. Nebo mám snad celý postup špatně?:) Děkuji.
Offline
- (téma jako vyřešené označil(a) Pajaa)
#2 27. 11. 2011 01:06 — Editoval Phate (27. 11. 2011 01:07)
Re: Derivace funkce v bodě
Ta limita ma byt pro h jde k nule a ne x. Jinak cesta zatim spravna, ted to uprav na jeden zlomek(s jednou zlomkovou carou) a vhodne rozsir, aby ses zbavila odmocnin v citateli. Pekne se ti pak odeckou acka a zustane tam jen h a to pokratis v citateli i jmenovali. A pak uz muzes s cistym svedomim poslat h k nule a vycislit :)
Vykonávat věc, které se bojíme, je první krok k úspěchu.
Offline
#7 27. 11. 2011 20:41 — Editoval ((:-)) (27. 11. 2011 20:42)
Re: Derivace funkce v bodě
↑ rendy139:
Prečo myslíš, že je číslo 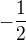 ako hodnota derivácie v bode 1 zle?
ako hodnota derivácie v bode 1 zle?
Derivácia tejto funkcie  je
je  .
.
Keď dosadíš za x číslo 1 (derivácia v bode 1), tak dostaneš tú 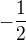 ...
...
Offline


 díky
díky a ne
a ne 




 mi vychází
mi vychází  , což si myslím, že je špatně..$
, což si myslím, že je špatně..$