Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 11. 2011 19:50
- (-anicka-)

- Zelenáč
- Příspěvky: 12
- Reputace: 0
L´Hospitalovo pravidlo
Prosim o pomoc s tymto prikladom.. vo vysledkoch mam e na 2 aa nejako k tomu nemozem dospiet... vopred dakujem :) ...![kopírovat do textarea $\lim_{x\to\infty }=[\frac{x^{2}+2x+2}{x^{2}+2}]^{x}$](/mathtex/16/16b5f52e6d891b605dc5bed8cd052ef8.gif)
Offline
#2 29. 11. 2011 19:53
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: L´Hospitalovo pravidlo
↑ (-anicka-):
Ahoj, využij toho, že 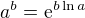 .
.
Offline
#3 29. 11. 2011 20:00
- (-anicka-)

- Zelenáč
- Příspěvky: 12
- Reputace: 0
Re: L´Hospitalovo pravidlo
↑ Pavel Brožek: aa no jasne :D ... dakujem ;)
Offline
#5 29. 11. 2011 22:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: L´Hospitalovo pravidlo
Mně se nepodařilo dle návodu od ↑ Pavel Brožek: dojit k výsledku jinak, než použitím l´Hospital. Proto jsem opět použila pozoruhodnou limitu. Když teď dostanu nařízení zdůvodňovat, tak už to bude horší - musela bych stát u klávesnice v pozoru :-) 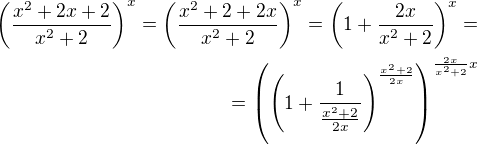
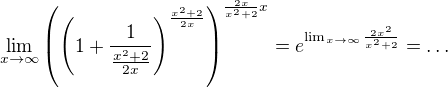
Když jsem dopsala, tak jsem si všimla titulku, že muže být l´Hospital :-) Myslím, že l´Hospital bude vysvětlen u Wolframu, případně dejte vědět, zda pokračovat.
Zdravím v tématu.
Offline