Matematické Fórum

u_peg · 28. 11. 2011 17:02

Dobrý deň.

Mám zhruba 27 miestne číslo ktoré vždy končí číslom 252950. Dve cifry pred 252950 mám zvoliť tak aby po delení číslom 97 bol zvyšok 1.

Ide o počítanie kontrolného súčtu pre portugalský IBAN http://en.wikipedia.org/wiki/Internatio … unt_Number

Nedarí sa mi vymyslieť sposob ako určiť tento kontrolný súčet.

Pavel Brožek · 29. 11. 2011 00:05

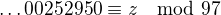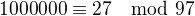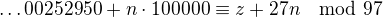Vzal bych si to číslo, na ta dvě místa před 252950 dal nuly a spočítal bych zbytek $z$ po dělení 97, tj. $\ldots00252950\equiv z\mod 97$ . Pak bych si snadno spočítal, že $1000000\equiv27\mod97$ . Takže když si vezmu dvouciferné číslo $n$ , tak bude $\ldots00252950+n\cdot100000\equiv z+27n\mod97$ . A já tedy chci 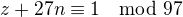$z+27n\equiv 1\mod97$ . Protože číslo inverzní k číslu 27 je 18 ( 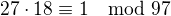$27\cdot18\equiv1\mod97$ ), vynásobím jím rovnost a dostanu

$18z+18\cdot27n&\equiv 18\mod97\\ 18z+n&\equiv18\mod97\\ n&\equiv18(1-z)\mod97$

Stačí mi tedy spočítat 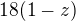$18(1-z)$ a přičíst k tomu vhodný násobek 97, aby n bylo kladné dvojciferné číslo.

u_peg · 30. 11. 2011 16:09

↑ Pavel Brožek:
Ďakujem za nakopnutie. Neviem ako to je matematicky. V počítači to funguje tak, že -1 mod 97 = -1 a teda bolo potrebné upraviť výpočet tak, že n = (18 * ((1 - z + 97) mod 97)) mod 97

Matematické Fórum

#1 28. 11. 2011 17:02

modulus algebra

#2 29. 11. 2011 00:05

Re: modulus algebra

#3 30. 11. 2011 16:09

Re: modulus algebra

Zápatí