Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 01. 12. 2011 20:57
Re: Limita
↑ Alivendes:Děkuju, tento způsob se zdá jednoduší než na 3x derivovat zvlášť zlomek.
Offline
#4 01. 12. 2011 21:07
Re: Limita
↑ comboxxx:
Nebo to stačí roztrhnout tak jak to je, derivace opravdu nejsou zapotřebí.
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#5 01. 12. 2011 21:50
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ Alivendes:
Zdravím,
už jsem prosila - buď tak hodný a umístí sem materiál, ze kterého tento postup doporučuješ. Nebo Tebe nahlásím Moderátorovi Ondřejovi - zakladateli Rychlokurzu. Já netvrdím, že je to nesprávně, ale neviděla jsem toto v osnovách SŠ (ale ani jinde). Děkuji.
↑ comboxxx:
možná cesta, napriklad (bez derivací):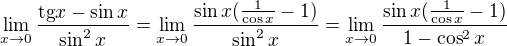
je vidět co dál. Děkuji.
Offline
#6 01. 12. 2011 21:53
Re: Limita
↑ jelena:
Není to v osnovách SŠ, konzultoval jsem to s naší profesorkou matematiky, prý si nepamatuje, jak se to dokazuje. Je to podle ní látka VŠ
Mám to od ní, když jsem počítal jednu limitu.
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#7 01. 12. 2011 21:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ Alivendes:
já věřím, že to dokázat jde (a nevadí, že to bude látka VŠ). Ale nemohu souhlasit, že tento postup zde budeš nabízet bez důkazu na oficiální zdroj. Není to žádný útok na Tvůj postup, ale rozumíme se - pochybuji, že to kolega může nabídnout jako řešení limity z Petákové.
Děkuji.
Offline
#9 02. 12. 2011 00:12
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ Alivendes:
děkuji, pokud bude důkaz, tak to bude jistě zajímavé (je možné, že ho zná nebo hravě provede i někdo z kolegů). Ale řekla bych, že i když bude uveřejněn zde na fóru, tak bych ho nenabízela jako oficiální postup. Na SŠ bychom se mohli např. držet postupů dle této sady učebnic. část Diferenciální a integrální počet.
Určitě to nespěchá, děkuji za ochotu :-)
Offline
#11 02. 12. 2011 09:18
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ jarrro:
Zdravím a děkuji,
samozřejmě, že ten vztah v úpravě vidím, ale naše debata vznikla zde (viz postup kolegy v příspěvku 2 a následná debata, že vzorec (sinx)/x nepoužívá). Tedy nesouhlasím s tvrzením bez důkazu:
použít to, že sinus a tangens se dá v okolí bodu nule aproximovat přímkou.
a se zápisem výsledku bez mezikroků (to je až u Tebe v příspěvku, kolega to nemá ani v náznaku). Souhlasíš? Děkuji.
Offline
#13 02. 12. 2011 10:32
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limita
↑ jarrro:
:-) Jaro, zlato naše, co my dva řešíme? Tobě je to jasné, mně je to jasné.
Kolega Alivendes nabizí středoškolakovi a Michalce (oba jsou u začátku limit) tvrzení o aproximaci přímkou, důkaz nemá, vzorec (sinx)/x nezná (nepoužívá). A jediné co má, že jedna paní si nepamatuje, jak se to dokazuje. Proto jsem se ozvala, rozumíš, prosím?
To máš tak - jsem velmi a velmi pro, aby zde bylo co nejvíce odpovědí středoškoláků. A aby od vás, naších elit, přicházel odborný mentoring a dohled, že něco není úplně košer (samozřejmě, ne ode mne - kde jsem viděla matematiku?). Vím, že nemáte čas a asi to ani nebaví.
Děkuji, měj se :-)
Offline
#15 02. 12. 2011 15:35
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita
Dobré odpoledne přeji,
naprosto nechápu postup z první odpovědi. Myslím tím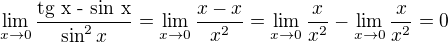
I kdybych tu danou aproximaci bral jakože je košér (podle mě není), tak další postup není algebraicky správně. V čitateli máme nulu, netřeba to rozdělovat. Když to rozdělíme, tak to je špatně, protože ani jedna z těch daných limit není definovaná. Žádná nula tedy nevyjde. Postup tedy určitě správně není, i kdybych akceptoval aproximaci.
---
"Aproximace přímkou" je 100% správně, pokud ji využijeme v kombinaci s aritmetikou limit a všechny limity během postupu existují. Pak člověk nemůže mít námitek.
Nahradit ale goniometrickou funkci funkcí lineární kdekoliv, to je dost odvážné. Používejte raději Taylorův rozvoj, který je vaší technice asi nejblíže. Asi to myslíte, jen nechcete psát ty další členy rozvoje, ty jsou tam ale dost podstatné.
Připomíná mi to kolegu vanoka, který počítal přes metodu ekvivalentů. Což je trochu paradoxní název, když to ekvivalentní moc není :-)
Offline
#16 02. 12. 2011 15:43
Re: Limita
↑ halogan:
Tak to napišme takhle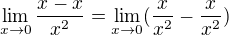
Nemůžeš popřít, že tohle se rovná nule ...
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#17 02. 12. 2011 15:51
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita
↑ Alivendes:
To nemohu. Mohu ale popřít validitu toho prvního kroku. Mám tu pro tebe jednu limitu: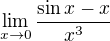
Tady přesně selže ta tvoje technika, protože ta "aproximace" má svoje dost striktní pravidla.
Offline
#18 02. 12. 2011 15:58
Re: Limita
↑ halogan:
No ...asi máš pravdu, že roztrhnutí je špatně jak tady, tak tam. Když jsme to počítal, tak jsme si nebyl uplně jistý tím, co jsem udělal když jsem to roztrhnul. Ale přepočítával jsem to normálně a kontroloval podle grafu a vyšlo to stejně, tak jsem to sem napsal.
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#19 02. 12. 2011 16:00
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Limita
↑ Alivendes:
Ono nejde o roztrnutí. Kdybych to počítal tvým způsobem, tak mám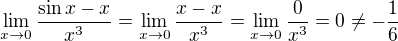
Klíč k rozlousknutí, proč tvá technika nefunguje, najdeš při studiu Taylorova rozvoje. Moc šikovná věc.
Offline


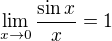 ,ale v tomto prípade to podľa mňa nie je použité celkom správne keď už tak skôr
,ale v tomto prípade to podľa mňa nie je použité celkom správne keď už tak skôr
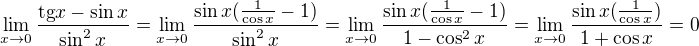
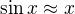 alebo je niekde problém?
alebo je niekde problém?