Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Svaz podprostorů vektorového prostoru je jednoduchý (TOTO TÉMA JE VYŘEŠENÉ)
#1 03. 12. 2011 17:57 — Editoval Andrejka3 (04. 12. 2011 00:29)
Svaz podprostorů vektorového prostoru je jednoduchý
Zadání:
Buď  vektorový prostor nad tělesem
vektorový prostor nad tělesem  dimenze aspoň 2. Dokažte, že svaz
dimenze aspoň 2. Dokažte, že svaz  jeho podprostorů je jednoduchý.
jeho podprostorů je jednoduchý.
Pojmy a označení:
Řešení pro prostory konečné dimenze:
Prosím, má někdo tušení, jak dokázat tvrzení pro prostory nekonečné dimenze?
Edit: úpravy textu + rozepsání Kroku 1 (Analogicky dostaneme...)
co je svaz a svazově usp. množ. Zde
Edit úplně dole:
What does a drowning number theorist say?
'log log log log ...'
Offline
- (téma jako vyřešené označil(a) Andrejka3)
#2 03. 12. 2011 18:44 — Editoval OiBobik (03. 12. 2011 18:45)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ Andrejka3:
Detail (asi přepis - anebo to už vůbec nechápu : D ):
Algebra je tedy jednoduchá, pokud má nějakou vlastní kongruenci.
v tom případě snad právě algebra jednoduchá není, ne?
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 03. 12. 2011 18:46
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ OiBobik:
Díky, přepis. Je jednoduchá, když nemá vlastní kongruenci.
What does a drowning number theorist say?
'log log log log ...'
Offline
#5 03. 12. 2011 21:04 — Editoval Pavel Brožek (03. 12. 2011 21:07)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Svaz podprostorů vektorového prostoru je jednoduchý
Algebra
má aspoň dvě kongruence (pokud nesplývají) a to identitu na
a
.
Tomuhle moc nerozumím. Pokud dobře chápu, tak jedna kongruence bude taková, že každý prvek bude kongruentní jen sám se sebou (tady celkem chápu, že se tahle kongruence dá zapsat jako „identita na  “). Druhá kongruence bude taková, že každý prvek bude kongruentní s každým. Pokud tahle kongruence má být „identita na
“). Druhá kongruence bude taková, že každý prvek bude kongruentní s každým. Pokud tahle kongruence má být „identita na 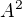 “, tak ten zápis „identita na
“, tak ten zápis „identita na 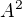 “ nechápu, můžeš ho prosím trochu vysvětlit?
“ nechápu, můžeš ho prosím trochu vysvětlit?
V tvém důkazu pro konečnou dimenzi nechápu krok 1 (ne, že bych ty další chápal, jen jsem se k nim zatím nedostal :-)). Asi mi není úplně jasné, co dokazuješ.  se snažíš dokázat nebo to z něčeho plyne (nevidím z čeho)? Pak nechápu (Edit: už asi chápu, je to důsledek
se snažíš dokázat nebo to z něčeho plyne (nevidím z čeho)? Pak nechápu (Edit: už asi chápu, je to důsledek  ), proč by mělo platit
), proč by mělo platit  , můžeš to prosím rozvést?
, můžeš to prosím rozvést?
Nyní můžeme psát:
Tady ti vypadly lomené závorky kolem  ?
?
Další dotazy asi budou následovat později… :-)
Offline
#6 03. 12. 2011 21:12 — Editoval Andrejka3 (03. 12. 2011 21:12)
Re: Svaz podprostorů vektorového prostoru je jednoduchý
omuhle moc nerozumím. Pokud dobře chápu, tak jedna kongruence bude taková, že každý prvek bude kongruentní jen sám se sebou (tady celkem chápu, že se tahle kongruence dá zapsat jako „identita na “). Druhá kongruence bude taková, že každý prvek bude kongruentní s každým. Pokud tahle kongruence má být „identita na “, tak ten zápis „identita na “ nechápu, můžeš ho prosím trochu vysvětlit?
Jistě, ráda. Nešťastně napsané. Myslela jsem relaci, kde všichni jsou kongruentní (ekvivalentní) se všemi, tedy celý kartézský součin nosné množiny se sebou samou, 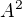 . Musím to editovat tak, aby to nebylo zavádějící.
. Musím to editovat tak, aby to nebylo zavádějící.
V tvém důkazu pro konečnou dimenzi nechápu krok 1 (ne, že bych ty další chápal, jen jsem se k nim zatím nedostal :-)). Asi mi není úplně jasné, co dokazuješ. se snažíš dokázat nebo to z něčeho plyne (nevidím z čeho)? Pak nechápu (Edit: už asi chápu, je to důsledek ), proč by mělo platit , můžeš to prosím rozvést?
Rozvedu to, je to trochu kódované mým kódem, takže to nemusí být úplně srozumitelné, napravím to.
Závorky tam chybí jedny.
What does a drowning number theorist say?
'log log log log ...'
Offline
#7 03. 12. 2011 21:22 — Editoval Andrejka3 (03. 12. 2011 21:31)
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ Pavel Brožek:
Už by mělo být srozumitelné, co je předpoklad a co ne. Toto jsem považovala za estetičtější, dát k tildě (
Toto jsem považovala za estetičtější, dát k tildě ( ) výsledky těch operací. Využívám jen toho, že
) výsledky těch operací. Využívám jen toho, že  a
a  jsou ekvivalentní a tedy jejich produkty s třetím objektem musí být taky ekvivalentní. Třetím objektem je
jsou ekvivalentní a tedy jejich produkty s třetím objektem musí být taky ekvivalentní. Třetím objektem je 
Edit: taky jsem rozepsala ten krok 1 : Analogicky dostaneme...
What does a drowning number theorist say?
'log log log log ...'
Offline
#8 03. 12. 2011 23:46
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Svaz podprostorů vektorového prostoru je jednoduchý
Do jisté míry už chápu tvůj důkaz, pro jistotu ho ale ještě trochu rozeberu.
Toto jsem považovala za estetičtější
Tohle mě hodně mátlo (i po tom, co jsem pochopil, jak to myslíš, tak mě to pořád pletlo) :-). Mnohem pochopitelnější by pro mě bylo napsat  . Tam každé
. Tam každé  a
a  odpovídá jedné elementární úpravě, která je evidentní. Jakmile si každou úpravu ověřím, už jen koukám na levý a pravý konec zápisu.
odpovídá jedné elementární úpravě, která je evidentní. Jakmile si každou úpravu ověřím, už jen koukám na levý a pravý konec zápisu.
Píšeš, že jednodimenzionální podprostory generují celý prostor. Už ale nedodáváš, že pokud  , pak i
, pak i  a
a  a díky tomu máme ekvivalenci na všech podprostorech. Asi ti to přijde zřejmé (já vím, je to jednoduché dokázat) a proto to nezmiňuješ, ale mě třeba podobné nevyslovené věci komplikují pochopení. (Zvlášť když se v tomhle oboru matematiky nepohybuji často a spousta věcí je pro mě nových.) :-)
a díky tomu máme ekvivalenci na všech podprostorech. Asi ti to přijde zřejmé (já vím, je to jednoduché dokázat) a proto to nezmiňuješ, ale mě třeba podobné nevyslovené věci komplikují pochopení. (Zvlášť když se v tomhle oboru matematiky nepohybuji často a spousta věcí je pro mě nových.) :-)
V kroku 4 – co když  . Pak bychom nemohli použít krok 3. Měli bychom tedy říct, že buď
. Pak bychom nemohli použít krok 3. Měli bychom tedy říct, že buď  nebo
nebo  (jinak by byl spor s
(jinak by byl spor s  ) a pak se podle toho zařídit.
) a pak se podle toho zařídit.
Teď už se snad budu moct zaměřit na vymýšlení důkazu pro nekonečnědimenzionální prostory. :-)
Offline
#9 04. 12. 2011 00:07
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ Pavel Brožek:
Mooc díky za Tvůj čas.
Pravda všechno, zkusím tam přidat ty věci.
What does a drowning number theorist say?
'log log log log ...'
Offline
#10 04. 12. 2011 00:39
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Svaz podprostorů vektorového prostoru je jednoduchý
Ať vidím, jestli má smysl pokračovat, tak sem napíšu, co zatím mám:
Předpokládejme, že  ,
,  jsou podprostory
jsou podprostory  . Dále předpokládejme, že
. Dále předpokládejme, že
(což je ekvivalentní tomu, že U a W nejsou jeden podprostorem druhého). Je zřejmé, že  jsou lineárně nezávislé vektory. Platí
jsou lineárně nezávislé vektory. Platí ,
,
máme tedy dva kongruentní jednorozměrné různé podprostory V. Dále platí
Stačí už jen použít tvůj krok 1, abychom zjistili, že každý jednodimenzionální podprostor V je kongruentní 0.
Samozřejmě to není dokončené a neřeším vůbec případ, že U a W bude jeden podprostorem druhého, ale je zatím to, co jsem napsal, správně?
Offline
#11 04. 12. 2011 00:44
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ Pavel Brožek:
Správně.
What does a drowning number theorist say?
'log log log log ...'
Offline
#12 04. 12. 2011 01:41
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Svaz podprostorů vektorového prostoru je jednoduchý
Dělal jsem to zbytečně složitě. Znovu:
Předpokládejme, že  ,
,  jsou podprostory
jsou podprostory  . Existuje tedy vektor
. Existuje tedy vektor  , který patří jen do jednoho z prostorů
, který patří jen do jednoho z prostorů  a
a  . Bez újmy na obecnosti nechť
. Bez újmy na obecnosti nechť 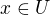 ,
,  . Pak
. Pak
Teď stačí použít krok 1. Víme tedy, že všechny konečnědimenzionální podprostory jsou kongruentní.
Offline
#13 04. 12. 2011 01:45 — Editoval Andrejka3 (04. 12. 2011 03:10)
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ Pavel Brožek:
Myslím, že to je skvělá cesta. Napadlo mě použít Zornovo lemma.
Odkaz
Označme  . Je každý řetězec této množiny shora omezený? Kdyby ano, pak bychom pokračovali:
. Je každý řetězec této množiny shora omezený? Kdyby ano, pak bychom pokračovali:
Důsledek lemmatu: pak existuje maximální prvek  .
.
Označme tento maximální prvek  .
.
Kdyby  nebylo
nebylo  , pak dostaneme spor s maximalitou prvku, protože existuje vektor, který nepatří do
, pak dostaneme spor s maximalitou prvku, protože existuje vektor, který nepatří do  , označme ho
, označme ho  . Dále označme bazi
. Dále označme bazi  jako
jako  a
a  prvek té baze.
prvek té baze.
Platí: , protože
, protože 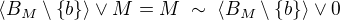 . Dále,
. Dále,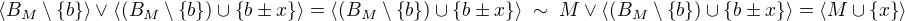 .
.
Myslím, že je  , takže jsme propojili třídy ekvivalence a je
, takže jsme propojili třídy ekvivalence a je  ale taky
ale taky  , což je spor s maximalitou
, což je spor s maximalitou  .
.
Jsou splněny předpoklady lemmatu?
What does a drowning number theorist say?
'log log log log ...'
Offline
#14 04. 12. 2011 02:38
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Svaz podprostorů vektorového prostoru je jednoduchý
Já už jdu spát, ale tipnul bych si, že bude problém dokázat, že bude každý řetězec shora omezený.
Offline
#15 04. 12. 2011 03:36
Re: Svaz podprostorů vektorového prostoru je jednoduchý
Ještě jsem přemýšlela.. Ty věci, co píšu o bazích nekonečně dimenzionálních prostorech nejspíš nebudou oprávněné. Když si vzpomenu na Lp prostory a jim podobné. Tam to asi tak jednoduše fungovat nebude.
Tak zatím,
dobrou.
What does a drowning number theorist say?
'log log log log ...'
Offline
#16 04. 12. 2011 11:16 — Editoval OiBobik (04. 12. 2011 11:21)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ Pavel Brožek:
Omezenost řetězců shora je "zadarmo", ne? Koneckonců, je to uspořádání inkluzí a všechny podprostory mají jako horní závoru celý prostor.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#17 04. 12. 2011 11:26
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ OiBobik:
To je sice pravda, ale nevím, jestli to tak lze použít, když nevíme, jestli V je v té množině K.
Třeba interval (0,1) je omezený shora číslem 1, ale sám interval maximální prvek nemá.
What does a drowning number theorist say?
'log log log log ...'
Offline
#18 04. 12. 2011 11:35
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ Andrejka3:
Pravda, uvažuju špatně.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#19 04. 12. 2011 12:19 — Editoval Pavel Brožek (04. 12. 2011 12:27)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Svaz podprostorů vektorového prostoru je jednoduchý
Pokud je  konečnědimenzionální, pak
konečnědimenzionální, pak  . Pro libovolné
. Pro libovolné  pak platí
pak platí  . Pokud tedy nekonečnědimenzionální podprostor „sjednotíme“ s konečnědimenzionálním, budou ten původní a sjednocený kongruentní.
. Pokud tedy nekonečnědimenzionální podprostor „sjednotíme“ s konečnědimenzionálním, budou ten původní a sjednocený kongruentní.
Offline
#20 04. 12. 2011 12:53
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ Pavel Brožek:
Tomu nerozumím. Nevím, co je levá strana v  .
.
Co když existuje kongruence taková, že v jedné třídě ekvivalence jsou dva nekonečnědimenzionální podprostory, jejichž průnik je opět nekonečnědimenzionální? A třeba třídy ekvivalence takové kongruence jsou jednoprvkové pro všechny konečnědimenzionální podprostory?
What does a drowning number theorist say?
'log log log log ...'
Offline
#21 04. 12. 2011 12:57
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Svaz podprostorů vektorového prostoru je jednoduchý
Mějme dva podprostory  prostoru
prostoru  . Označme
. Označme  bázi
bázi  . Bázi
. Bázi  můžeme doplnit na bázi
můžeme doplnit na bázi  prostoru
prostoru  a na bázi
a na bázi  prostoru
prostoru  . Pak platí
. Pak platí  . Označme
. Označme  a
a  . Řekneme, že prostory
. Řekneme, že prostory  a
a  se liší o prostor konečné dimenze, pokud
se liší o prostor konečné dimenze, pokud  a
a  jsou konečné množiny.
jsou konečné množiny.
Proč pak není „ právě tehdy když se
právě tehdy když se  a
a  liší o prostor konečné dimenze“ kongruencí?
liší o prostor konečné dimenze“ kongruencí?
Offline
#22 04. 12. 2011 13:01
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ Andrejka3: a
a  jsou podprostory
jsou podprostory  . Písmenem
. Písmenem  teď nemyslím algebru nebo něco jiného. Má tedy smysl psát
teď nemyslím algebru nebo něco jiného. Má tedy smysl psát  . Z definice kongruence a předpokladu, že
. Z definice kongruence a předpokladu, že  je konečnědimenzionální (tj.
je konečnědimenzionální (tj.  , jak jsme ukázali dříve), plyne
, jak jsme ukázali dříve), plyne  .
.
Offline
#23 04. 12. 2011 13:05
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ Pavel Brožek:
Budu se snažit to promyslet, jen mi to trochu asi potrvá.
What does a drowning number theorist say?
'log log log log ...'
Offline
#24 04. 12. 2011 13:05 — Editoval Olin (04. 12. 2011 13:07)
Re: Svaz podprostorů vektorového prostoru je jednoduchý
Pavel Brožek napsal(a):
Píšeš, že jednodimenzionální podprostory generují celý prostor. Už ale nedodáváš, že pokud
, pak i
a
a díky tomu máme ekvivalenci na všech podprostorech.
Omlouvám se za vracení k takto starým věcem, ale tuto větu jsem nepochopil. "Máme ekvivalenci na všech podprostorech" má znamenat, že už jsou všechny ekvivalentní?
Jinak mám už od včerejšího večera strašný pocit, že
by měla být vlastní kongruence na nekonečnědimenzionálním prostoru, jen to nemám úplně doladěné.
EDIT: Jejda, teď jsem si všiml, že kolega BrozekP nastínil tu samou myšlenku.
Offline
#25 04. 12. 2011 13:11
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Svaz podprostorů vektorového prostoru je jednoduchý
↑ Olin:
Ta citace se týkala důkazu pro  konečné dimenze. Takže pokud víme, že každý jednodimenzionální podprostor
konečné dimenze. Takže pokud víme, že každý jednodimenzionální podprostor  je ekvivalentní nulovému podprostoru, a že „sjednocení“ a průnik dvou ekvivalentních podprostorů
je ekvivalentní nulovému podprostoru, a že „sjednocení“ a průnik dvou ekvivalentních podprostorů  je ekvivalentní
je ekvivalentní  , pak by měl být každý podprostor
, pak by měl být každý podprostor  ekvivalentní nulovému podprostoru.
ekvivalentní nulovému podprostoru.
Tohle je asi jen hezky zapsané to, co jsem se snažil napsat ↑ tady:. Takže máme stejný pocit :-).
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Svaz podprostorů vektorového prostoru je jednoduchý (TOTO TÉMA JE VYŘEŠENÉ)
 je množina všech podprostorů prostoru
je množina všech podprostorů prostoru 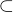 je uspořádaná. Dokonce je uspořádaná svazově, protože
je uspořádaná. Dokonce je uspořádaná svazově, protože
 , kde operace jsou binární a znamenají infimum, resp. supremum.
, kde operace jsou binární a znamenají infimum, resp. supremum.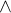 ) platí:
) platí: a soucasne
a soucasne  , pak
, pak  .
. a soucasne
a soucasne 
 a ekvivalenci
a ekvivalenci  Z tohoto předpokladu chci vyvodit, že pak každý podprostor je v relaci s každým a že se tedy jedná o nevlastní kongruenci,
Z tohoto předpokladu chci vyvodit, že pak každý podprostor je v relaci s každým a že se tedy jedná o nevlastní kongruenci,  ..
..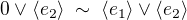 )))
))) jsou nezávislé.
jsou nezávislé. . Rozepíšu to:
. Rozepíšu to:
 (vypada to jako stara trolej tramvaje v Hasse diagram nebo jako sprosty obrazek damskeho prirozeni či značky francouzského výrobce aut), jsou tedy všechny jednodimenzionální podprostory ekvivalentní a ekvivalentní s nulovým podprostorem. Tato množina ale generuje
(vypada to jako stara trolej tramvaje v Hasse diagram nebo jako sprosty obrazek damskeho prirozeni či značky francouzského výrobce aut), jsou tedy všechny jednodimenzionální podprostory ekvivalentní a ekvivalentní s nulovým podprostorem. Tato množina ale generuje 
 . Toto je dle předpokladu ekvivalentní s
. Toto je dle předpokladu ekvivalentní s  .
. . Je-li
. Je-li  , pak se na Krok 2 dostaneme jednoduše tak, že zřejmě můžeme psát
, pak se na Krok 2 dostaneme jednoduše tak, že zřejmě můžeme psát  ,
,  . Pak totiz pro
. Pak totiz pro  platí:
platí: .
. , pak pokud jeden podprostor je podprostorem druhého, můžeme rovnou jít na Krok 3. V opačném případě
, pak pokud jeden podprostor je podprostorem druhého, můžeme rovnou jít na Krok 3. V opačném případě  , a do Kroku 3 jdeme s dvojicí
, a do Kroku 3 jdeme s dvojicí  , čímž jsme obecný případ převedli na Krok 3.
, čímž jsme obecný případ převedli na Krok 3.