Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 11. 2011 23:03
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Dynamika soustavy těles
Zdravím a prosím o kontrolu řešení jedné úlohy. Máme dvě tělesa podle obrázku a úkolem je určit zrychlení hmotného bodu m a tělesa M a reakční síly, vše jako funkci  a rozměrů. Všechny pohyby probíhají bez tření.
a rozměrů. Všechny pohyby probíhají bez tření.
Obrázek:
Až teď jsem si všimnul, že reakci podložky značím R, což už je poloměr, který teda místo R označím r.
Moje úvaha: Ve směru osy x nepůsobí žádná vnější síla, takže těžiště soustavy nebude zrychlené (nebo taky zákon zachování hybnosti). Početně:
(1)
 .
.Mezi souřadnicemi pak platí vztahy:
(2)
 a
a(3)
 . Po dosazení (3) do (2) a dvojí derivaci podle času:
. Po dosazení (3) do (2) a dvojí derivaci podle času:(4)

Dosazením (4) do (1) a vyřešením pro
 :
:
pak už jde snadno dopočítat:

Dosazením do rovnic na obrázku:
 ,
, .
.Děkuji za kritickou kontrolu.
Offline
- (téma jako vyřešené označil(a) FliegenderZirkus)
#2 29. 11. 2011 00:33 — Editoval Pavel Brožek (29. 11. 2011 01:10)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
↑ FliegenderZirkus:
Nevidím v tom chybu.
Ještě než jsem prošel tvůj postup, zkusil jsem si sestavit sám Lagrangeovy pohybové rovnice pomocí zobecněných souřadnic  . Z pohybové rovnice pro
. Z pohybové rovnice pro  mi samozřejmě vyšel stejně jako tobě zákon zachování hybnosti. Z druhé pohybové rovnice mi vyšlo
mi samozřejmě vyšel stejně jako tobě zákon zachování hybnosti. Z druhé pohybové rovnice mi vyšlo
Normálové síly jsem už nepočítal. Tak je otázka, jestli se tvůj a můj výsledek na sebe dají převést nebo tam někdo z nás má chybu. Tipoval bych první možnost.
Edit: Tvé vyjádření  vlastně vychází pouze ze zákona zachování hybnosti. Mé vyjádření vychází z druhé pohybové rovnice. Je tedy logické, že to vypadá jinak, a teprve kdyby se tam dosadilo řešení
vlastně vychází pouze ze zákona zachování hybnosti. Mé vyjádření vychází z druhé pohybové rovnice. Je tedy logické, že to vypadá jinak, a teprve kdyby se tam dosadilo řešení  , tak by to mělo přejít na stejný tvar.
, tak by to mělo přejít na stejný tvar.
Offline
#3 29. 11. 2011 11:17 — Editoval FliegenderZirkus (29. 11. 2011 22:48)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Dynamika soustavy těles
↑ Pavel Brožek:
Lagrangeovy rovnice budeme probírat zanedlouho, zatím tomu ale příliš nerozumím. Kdybych doplnil zadání tím, že: ,
,
tak už by mělo jít spočítat  , že? A tím pádem i ostatní veličiny jako funkce času. Zkusil jsem to takhle:
, že? A tím pádem i ostatní veličiny jako funkce času. Zkusil jsem to takhle: , h je výška tělesa M.
, h je výška tělesa M. . Zároveň máme
. Zároveň máme  spočítané z 2. Newtonova zákona (zapomněl jsem předtím tu rovnici napsat):
spočítané z 2. Newtonova zákona (zapomněl jsem předtím tu rovnici napsat): , z čehož plyne diferenciální rovnice pro
, z čehož plyne diferenciální rovnice pro  :
:
Tuhle rovnici asi jen tak vyřešit nepůjde, že?
EDIT: Oprava chyby červeně
Offline
#4 29. 11. 2011 11:30 — Editoval Pavel Brožek (29. 11. 2011 11:33)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
↑ FliegenderZirkus:
Nesedí ti v rovnicích jednotky. Už na začátku má být  . Ta výsledná rovnice vypadá podobně jako moje, pokud si to opravíš, tak nejspíš stejně. Pochybuji, že půjde analyticky vyřešit (Mathematica to nezvládla). Maximum, co jsem z ní zatím dostal, je perioda malých kmitů okolo
. Ta výsledná rovnice vypadá podobně jako moje, pokud si to opravíš, tak nejspíš stejně. Pochybuji, že půjde analyticky vyřešit (Mathematica to nezvládla). Maximum, co jsem z ní zatím dostal, je perioda malých kmitů okolo  :-). Pokud bych ji měl nějak řešit, tak bych asi zkusil přejít k proměnné
:-). Pokud bych ji měl nějak řešit, tak bych asi zkusil přejít k proměnné  (aby to vypadalo symetričtěji), pak si napsal řešení ve tvaru řady a snažil se najít vztahy mezi koeficienty řady.
(aby to vypadalo symetričtěji), pak si napsal řešení ve tvaru řady a snažil se najít vztahy mezi koeficienty řady.
Offline
#5 29. 11. 2011 12:17
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Dynamika soustavy těles
↑ Pavel Brožek:
Nojo, poloměr mi vypadl. Na řady si netroufám, zkusím to nějak převést na soustavu dvou rovnic prvního řádu a vyřešit přibližně pomocí Runge-Kutta, jestli to půjde. Např. pro  ,
,  ,
,  . Nejspíš ale až zítra..díky za spolupráci.
. Nejspíš ale až zítra..díky za spolupráci.
Offline
#6 29. 11. 2011 16:35 — Editoval Pavel Brožek (29. 11. 2011 18:10)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
↑ FliegenderZirkus:
Stále tam máš chybu – podle mě jsi zapoměl krátit m při počítání  z 2. Newtonova zákona. A ani potom mi to nevychází stejně. Uvedu svůj postup (nedostanu se ale k diferenciální rovnici druhého řádu, díky integrálům pohybu se jí vyhnu), ať případně můžeš hledat i ty chybu v mém.
z 2. Newtonova zákona. A ani potom mi to nevychází stejně. Uvedu svůj postup (nedostanu se ale k diferenciální rovnici druhého řádu, díky integrálům pohybu se jí vyhnu), ať případně můžeš hledat i ty chybu v mém.
Budu používat dvě zobecněné souřadnice  , kde
, kde  bude to samé jako
bude to samé jako  (tohle přeznačení dělám jen pro to, abych se nemusel stále vypisovat s indexem).
(tohle přeznačení dělám jen pro to, abych se nemusel stále vypisovat s indexem).
Zřejmě platí následující vztahy, které budu v průběhu výpočtu používat:
Vyjádřím si kinetické energie:
Vyjádřím si potenciální energii:
Lagrangián je
Je vidět, že lagrangián nezávisí explicitně na  , souřadnice
, souřadnice  je tedy cyklická a máme jeden integrál pohybu (hybnost ve směru x):
je tedy cyklická a máme jeden integrál pohybu (hybnost ve směru x):
Dále vidíme, že lagrangián nezávisí explicitně na čase, zobecněná energie proto bude také integrálem pohybu:
Nastavíme-li počáteční podmínky  , dostaneme
, dostaneme  a
a  .
.
Máme tak dvě rovnice, které musí funkce  splňovat:
splňovat:
Z první si vyjádřím  , dosadím do druhé a nakonec vyjádřím
, dosadím do druhé a nakonec vyjádřím  .
.
Pro přehlednost si zaveďme parametr  . Pak se rovnice zjednoduší na
. Pak se rovnice zjednoduší na
kde jsem označil  a
a  .
.
Tahle diferenciální rovnice asi nepůjde nějak hezky analyticky vyřešit. Když si to separuji, a nechám Mathematicu spočítat ten integrál, co tam vznikne, tak mi vrací nějaké hrozně složité funkce.
Offline
#7 29. 11. 2011 22:48
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Dynamika soustavy těles
↑ Pavel Brožek:
Prošel jsem si tvoje řešení krok po kroku a úpravám rozumím, i výpočtu potenciální a kinetické energie, akorát mi ještě chybí znalosti teorie, abych chápal, proč se kde derivuje Lagrangián a co to fyzikálně znamená. Na přednášce se k tomu dostaneme snad ještě do Vánoc, sice teda v němčině, ale něco z toho snad pochytím a projdu si tvůj výpočet ještě jednou.
Kromě nevykráceného  jsem zatím chybu ve svém řešení nenašel a vzorové bohužel nemám. S číselnými hodnotami uvedenými výše jsem tu rovnici napsal do Wolframu: Odkaz. Graf by mohl dávat smysl, ale to ještě nic neznamená. Zkusím porovnat přibližná řešení té mojí a tvojí rovnice.
jsem zatím chybu ve svém řešení nenašel a vzorové bohužel nemám. S číselnými hodnotami uvedenými výše jsem tu rovnici napsal do Wolframu: Odkaz. Graf by mohl dávat smysl, ale to ještě nic neznamená. Zkusím porovnat přibližná řešení té mojí a tvojí rovnice.
Offline
#8 29. 11. 2011 23:01
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
↑ FliegenderZirkus:
Kdyby tě to zajímalo a chtěl ses na to třeba podívat dopředu, tak dobrý studijní text k tomu je text k přednášce Teoretická mechanika od Jiřího Langera a Jiřího Podolského.
Offline
#9 29. 11. 2011 23:07
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Dynamika soustavy těles
↑ Pavel Brožek:
Určitě se podívám.
Mám trochu problém s tím, že můj výraz pro velikost reakce  není definovaný pro
není definovaný pro  , ačkoli fyzikálně nevidím důvod, proč by zrovna s tímhle úhlem měl být problém. Může být chyba někde tady?
, ačkoli fyzikálně nevidím důvod, proč by zrovna s tímhle úhlem měl být problém. Může být chyba někde tady?
Offline
#10 29. 11. 2011 23:28
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
↑ FliegenderZirkus:
Když si dosadíš  do rovnice na obrázku, z které jsi vypočítal
do rovnice na obrázku, z které jsi vypočítal  , dostaneš
, dostaneš
Je tedy jasné, že z této rovnice spočítat nepůjde. Limitu udělat nemůžeme, protože neznáme chování  . Tak to dopočítáme z druhé pohybové rovnice:
. Tak to dopočítáme z druhé pohybové rovnice:
Tady už problém v  není.
není.
Offline
#11 29. 11. 2011 23:45
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
Ještě jsem to překontroloval a máme tu výslednou rovnici pro  druhého řádu stejnou. Buď jsem udělal chybu, když jsem to předtím počítal, nebo to jen chtělo trochu víc manipulovat s goniometrickýma funkcema.
druhého řádu stejnou. Buď jsem udělal chybu, když jsem to předtím počítal, nebo to jen chtělo trochu víc manipulovat s goniometrickýma funkcema.
Offline
#12 02. 12. 2011 21:35 — Editoval FliegenderZirkus (02. 12. 2011 21:43)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Dynamika soustavy těles
↑ Pavel Brožek:
Tak jsem si napsal program na numerické řešení svojí rovnice
a graf vypadá stejně jako podle Wolfram Alpha. Pořád ale mám problém s  , nedokážu tu rovnici přepsat tak, aby s tím úhlem problém nebyl, řešení mám tedy jen pro
, nedokážu tu rovnici přepsat tak, aby s tím úhlem problém nebyl, řešení mám tedy jen pro  .
.
Když jsem numericky řešil rovnici  ,
,
tak mi vyšlo konstantní řešení  . Ještě se nad tím zamyslím, zatím jsem postupoval tak trochu bezmyšlenkovitě. :-)
. Ještě se nad tím zamyslím, zatím jsem postupoval tak trochu bezmyšlenkovitě. :-)
EDIT: Protože jsem použil krok 0,01, tak se problematickému bodu  „vyhnu“ a řešení mi vyjde pro libovolný interval, přesto se mi to ale nelíbí.
„vyhnu“ a řešení mi vyjde pro libovolný interval, přesto se mi to ale nelíbí.
Offline
#13 02. 12. 2011 21:57 — Editoval Pavel Brožek (02. 12. 2011 22:04)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
↑ FliegenderZirkus:
Mně ta tvá rovnice po úpravě vychází
tam by neměl být žádný problém v  nebo snad je? (Edit: Samozřejmě postup vynásobení kosinem je pochybný, takže by bylo vhodné jiným způsobem ukázat, že
nebo snad je? (Edit: Samozřejmě postup vynásobení kosinem je pochybný, takže by bylo vhodné jiným způsobem ukázat, že  pro
pro  . Já se tomuto problému ve svém postupu úplně vyhnu.)
. Já se tomuto problému ve svém postupu úplně vyhnu.)
Rovnici
jsme dostali pouze ze zákonů zachování hybnosti a energie. Ty určitě budou zachovány i když tam bude kulička viset ve vzduchu na místě :-). Druhá pohybová rovnice nám ale říká, že tam viset nebude.
Edit: Oprava chyby v první rovnici.
Offline
#14 02. 12. 2011 23:34
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Dynamika soustavy těles
↑ Pavel Brožek:
Jestli víme, že  pro
pro  , tak už je mi to jasné.
, tak už je mi to jasné.
Vzpomínám si na větu o postačujících podmínkách pro existenci a jednoznačnost řešení Cauchyovy (počáteční) úlohy. Požadovala se tam snad spojitost  . V našem případě tahle derivace v nule asi neexistuje? Nebo jak zdůvodnit, že řešení neni jednoznačné? A kolik jich tedy je, jen dvě? :-)
. V našem případě tahle derivace v nule asi neexistuje? Nebo jak zdůvodnit, že řešení neni jednoznačné? A kolik jich tedy je, jen dvě? :-)
Offline
#15 03. 12. 2011 00:27 — Editoval Pavel Brožek (03. 12. 2011 00:28)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
↑ FliegenderZirkus:
Pokud je funkce lipschitzovská, pak je řešení jednoznačné (Picard–Lindelöf theorem).  se pro malé
se pro malé  chová jako
chová jako  , odmocnina v okolí nuly ale lipschitzovská není.
, odmocnina v okolí nuly ale lipschitzovská není.
Řešení rovnice  s počáteční podmínkou
s počáteční podmínkou  je nekonečně mnoho – do času
je nekonečně mnoho – do času  těleso „visí“ ve vzduchu a pak začne padat.
těleso „visí“ ve vzduchu a pak začne padat.  můžeme volit jak chceme. Jakmile ale začne padat, tak je řešení jednoznačné až do doby, než nastane
můžeme volit jak chceme. Jakmile ale začne padat, tak je řešení jednoznačné až do doby, než nastane  . Tam se může těleso zastavit na libovolně dlouhou dobu a pak zase pokračovat kmitem zpátky do počáteční polohy. A tak dál.
. Tam se může těleso zastavit na libovolně dlouhou dobu a pak zase pokračovat kmitem zpátky do počáteční polohy. A tak dál.
Je potřeba využít toho, že máme ještě další pohybovou rovnici, které takové chování vylučuje a řešení nakonec bude jednoznačné. Funkce  z rovnice
z rovnice  je v proměnných
je v proměnných  a
a  lipschitzovská a je spojitá v proměnné t (triviálně – na t přímo nezávisí).
lipschitzovská a je spojitá v proměnné t (triviálně – na t přímo nezávisí).
Offline
#16 03. 12. 2011 10:57
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Dynamika soustavy těles
↑ Pavel Brožek:
Tak tohle je hodně zajímavé, taková jednoduchá úloha a člověk se toho tolik naučí. :-) V podstatě tomu už rozumím, ale:
Pavel Brožek napsal(a):
Řešení rovnice
s počáteční podmínkou
(...)
1) Můžu předepsat rovnici prvního řádu dvě počáteční podmínky?  mi vyjde dosazením, ne?
mi vyjde dosazením, ne?
2) To „správné“ řešení (alespoň pro první kmit) by šlo vynutit podmínkou  podle druhé rovnice, že? Zkusím to nějak propašovat do svého numerického řešení, ale zatím moc nevím jak.
podle druhé rovnice, že? Zkusím to nějak propašovat do svého numerického řešení, ale zatím moc nevím jak.
Offline
#17 03. 12. 2011 11:20
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
↑ FliegenderZirkus:
1) Máš pravdu, moje nepozornost.
2) To by snad mělo stačit. Možná bych to udělal tak, že pro malé hodnoty  bych to řešil tou rovnicí druhého řádu. Rovnice
bych to řešil tou rovnicí druhého řádu. Rovnice  tam asi bude dělat víc problémů než jen nejednoznačnost řešení – při numerickém řešení by nám mohlo vyjít i
tam asi bude dělat víc problémů než jen nejednoznačnost řešení – při numerickém řešení by nám mohlo vyjít i  a pak co s tím… :-)
a pak co s tím… :-)
Offline
#18 03. 12. 2011 11:35
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Dynamika soustavy těles
↑ Pavel Brožek:
Chtěl jsem se omezit jen na ![kopírovat do textarea $\varphi \in [0,\pi]$](/mathtex/a7/a7f31cebd86b6393714acd561a0c8217.gif) a pak nějak pochybně argumentovat symetrií. Pro vhodnou volbu
a pak nějak pochybně argumentovat symetrií. Pro vhodnou volbu 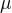 pak problém nenastane. :-)
pak problém nenastane. :-)
Řešit  jsem chtěl proto, abych ověřil, jestli vyjde stejná funkce
jsem chtěl proto, abych ověřil, jestli vyjde stejná funkce  jako z té rovnice druhého řádu. Jakmile je začnu nějak kombinovat, tak už to nebude tak věrohodné.
jako z té rovnice druhého řádu. Jakmile je začnu nějak kombinovat, tak už to nebude tak věrohodné.
Zkusím spíš udělat nějakou animaci a kdyžtak pošlu odkaz na video.
Offline
#19 03. 12. 2011 11:44
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
↑ FliegenderZirkus:
Pokud chceš porovnat řešení, tak zkus místo  začít s
začít s  (
( malé kladné).
malé kladné).
Offline
#20 03. 12. 2011 13:27
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
↑ FliegenderZirkus:
Tak jsem si hrál :-)
( ,
,  ,
,  ,
,  , průběh animace by měl být v reálném čase)
, průběh animace by měl být v reálném čase)
Offline
#21 04. 12. 2011 00:39 — Editoval FliegenderZirkus (04. 12. 2011 01:16)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Dynamika soustavy těles
↑ Pavel Brožek:
Jak se ti to povedlo stihnout tak rychle? Já svoji animaci dělal celý den. :-) Možná není Matlab ten pravý nástroj, ale spíš jen neznám správné postupy, můj kód je naprosto zběsilý. Perioda mi vyšla kolem  , tvoje animace mi přijde rychlejší, možná jen nepřesné časování těch gifů? Tam jsem zaokrouhloval dost.
, tvoje animace mi přijde rychlejší, možná jen nepřesné časování těch gifů? Tam jsem zaokrouhloval dost.
Lepší kvalita, ale větší soubor než 300 kB, takže jinde:
Graf závislosti úhlu na čase:
Graf závislosti
 na čase:
na čase:Trajektorie hmotného bodu m:
Offline
#22 04. 12. 2011 00:47 — Editoval FliegenderZirkus (04. 12. 2011 00:48)
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Dynamika soustavy těles
↑ FliegenderZirkus:
Možná přihlásím svůj zdroják do soutěže o nejnepřehlednější a nejpomalejší kód, jestli taková soutěž existuje. :-) Ale funguje to.
Offline
#23 04. 12. 2011 00:58
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Dynamika soustavy těles
Když jsem se teď v rychlosti podíval na graf, tak mi perioda vyšla asi 2.31s. Když jsem se stopkami změřil periodu (měřil jsem 20 period), tak mi vyšlo 2,12s. Takže tam někde budu mít chybu.
Na odkazu je zdrojový soubor k mé animaci:
http://dl.dropbox.com/u/5906979/soustava.nb
Pokud nemáš Mathematicu, tak obrázek:
Na to, že jsem se nesnažil o hezký kód, mi přijde celkem jednoduchý.
Offline
#24 04. 12. 2011 01:04
- FliegenderZirkus

- Příspěvky: 544
- Škola: RWTH Aachen
- Reputace: 25
Re: Dynamika soustavy těles
↑ Pavel Brožek:
To vypadá pěkně. Já bohužel k Mathematice nemám legální přístup, zkusím ale dostupnost licencí na ČVUTu ještě lépe prozkoumat.
Offline




