Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 12. 2011 13:56
- Sam_Hawkins
- Příspěvky: 44
- Reputace: 1
Příklad - dynamika tuhého tělesa
Dobrý den, mám tu příklad na dynamiku tuhého tělesa a vzhledem k tomu že nemám k dispozici výsledek, chtěl jsem ověřit správnost postupu:
Zadání:
Na dvojité naklonené rovine s úhly sklonu  a
a  jsou nehmotným nepružným vláknem pres válcovou kladku o hmotnosti m a poloměru r spojena tělesa o hmotnostech
jsou nehmotným nepružným vláknem pres válcovou kladku o hmotnosti m a poloměru r spojena tělesa o hmotnostech 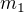 a
a 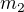 . Jaké je zrychlení soustavy? Odpor prostředí zanedbejte. (Moment setrvačnosti kladky je
. Jaké je zrychlení soustavy? Odpor prostředí zanedbejte. (Moment setrvačnosti kladky je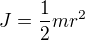 .)
.)
I. impulzová věta:
1. těleso :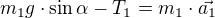
2. těleso :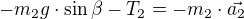
II. impulzová věta:
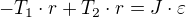
a za předpokladu že lanko je dokonale pevné (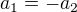 ) a nepodkluzuje (
) a nepodkluzuje (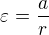 ) mám tři rovnice o třech neznámých (
) mám tři rovnice o třech neznámých (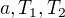 ) kterou dopočítám
) kterou dopočítám
moc si nejsem jistý jestli jsem dobře sestavil ty první dvě rovnice, resp. při přechodu z vektorového do skalárního tvaru...
předem díky za odpověď
P.S.: Ještě jsem si vzpomněl na jednu úlohu, tentokrát na zákon zachování:
Auto o počáteční rychlosti  brzdí po nakloněné rovině o sklonu
brzdí po nakloněné rovině o sklonu  (směrem dokopce). Jakou dráhu ještě urazí, je-li součinitel dynamického tření mezi koly a podložkou f?
(směrem dokopce). Jakou dráhu ještě urazí, je-li součinitel dynamického tření mezi koly a podložkou f?
- tady jsem uvažoval tak že počáteční kinetická energie auta se při prždění mení na práci vykonanou třecími silami a potenciální energii:
Pokud si zvolím hladinu nulové potencialní energie výšku auta, kde se nacházelo v okamžiku sepnutí brzd, platí:
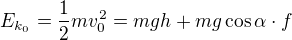 z čehož vyjádřím h dopočítám příslušnou vzdálenost.
z čehož vyjádřím h dopočítám příslušnou vzdálenost.
Offline
- (téma jako vyřešené označil(a) zdenek1)
#2 04. 12. 2011 17:26
Re: Příklad - dynamika tuhého tělesa
↑ Sam_Hawkins: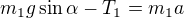
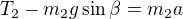
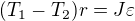
U toho druhého je myšlenka správně, ale 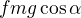 NENÍ práce, ale jen třecí síla. Musíš vynásobit dráhou.
NENÍ práce, ale jen třecí síla. Musíš vynásobit dráhou.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
