Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 12. 2011 16:57
- Nanoliquid

- Příspěvky: 64
- Reputace: 0
Určete největší obsah lichoběžníku
Dobrý den, potřeboval bych prosím pomoct s postupem u příkladu zadaným takto:
Mezi všemi rovnoramennými lichoběžníky vepsanými do daného pùlkruhu o poloměru R
tak, že jejich delší základna je průměr pùlkruhu, vyberte ten, který má největší obsah.
Určete rozměry lichoběžníka.
Vůbec si nevím rady a ani nevím, jak začít.
Offline
#2 08. 12. 2011 17:18
Re: Určete největší obsah lichoběžníku
↑ Nanoliquid:
Zdravím takéž. Zvolme pevně R > 0. Každý z lichoběžníků, o nichž je v úloze řeč, je jednoznačně určen svojí výškou  ,
,
proto i jeho obsah je funkcí proměnné  . Je potřeba analyticky vyjádřit tuto funkci a najít její absolutní maximum -
. Je potřeba analyticky vyjádřit tuto funkci a najít její absolutní maximum -
metodami pro vyšetřování průběhu funkce či jinak.
Offline
#3 08. 12. 2011 17:25
- Nanoliquid

- Příspěvky: 64
- Reputace: 0
Re: Určete největší obsah lichoběžníku
Takže podle vzorce obsahu lichoběžníka hledám S jako proměnnou y ?? 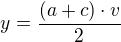 ?? a hledám lokální extrém této funkce ??
?? a hledám lokální extrém této funkce ??
Offline
#4 08. 12. 2011 17:31
Re: Určete největší obsah lichoběžníku
Ahoj ↑ Nanoliquid:,
Vyries najprv tvoj problem pre jednotkovu kruznicu z centrom v O.... a vyber
jeden vrchol lichobeznika A(cos x,sin x) v pravom kvadrate.
To premeni tvoj problem na studium maxima jednej funkcie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 08. 12. 2011 19:53
- Nanoliquid

- Příspěvky: 64
- Reputace: 0
Re: Určete největší obsah lichoběžníku
Nějak nerozumím ....Neměl bych ten bod A zvolit v v -1 na jednotkové kružnici, když má mít základna délku rovnou průměru ?? ... A k čemu mi vlastně je sin či cos ,? :(
Offline
#6 08. 12. 2011 20:18
Re: Určete největší obsah lichoběžníku
↑ Nanoliquid:,
urob si obrazok
bazu mas danu (oznacme ju CD)
A je bod malej bazy na kruhu, a automaticky jej druhy bod (oznacme ho B) taky ze A a B su symetricke podla osy y.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 08. 12. 2011 20:52
- Nanoliquid

- Příspěvky: 64
- Reputace: 0
Re: Určete největší obsah lichoběžníku
Tak jsem si udělal obrázek ....znamená to, že bod C je mezi 2. a 3. kvadrantem a d mezi 4. a 1. ?? body A a B jsou v prvním a druhém kvadrantu .. Chápu to správně ??
Offline
#8 08. 12. 2011 23:11
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Určete největší obsah lichoběžníku
↑ Nanoliquid:
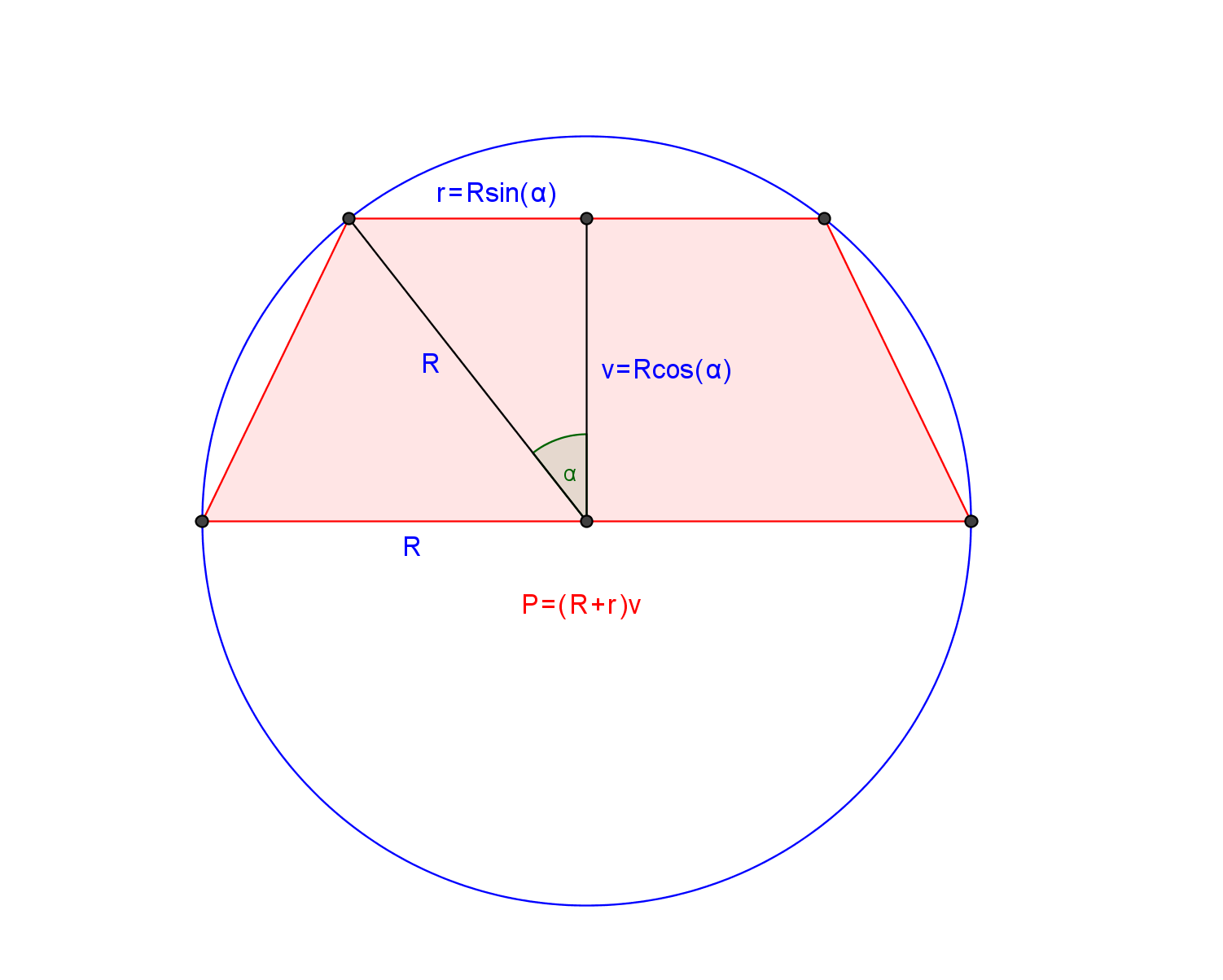
Pokud je střed souřadnic je zároveň středem kruhu (0, 0), potom body na poloměru jsou C (-r, 0), D(r, 0). Ze středu k vrcholu A (který je v prvním kvadrantu) udělám přímku (vzdálenost OA=r. Bude nás zajímat úhel DOA, jehož velikost bude ovlivňovat výšku lichoběžníku a délku strany AB. Tak nějak:
B______________A
/ \
C----------O---------D
Souhlasí? Děkuji.
Offline
#10 09. 12. 2011 09:19
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Určete největší obsah lichoběžníku
↑ Nanoliquid:
:-) Zakladatel definuje sinus(alfa) jako "délka protiléhlé odvesny/Délka přepony", tedy ve Tvém případě 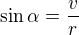 (alfa je DOA).
(alfa je DOA).
OT: "zdá se, že je opraveno značení pod obrázkem "trojúhelník s vyznačeným úhlem beta", děkuji autorovi.
Offline
#11 09. 12. 2011 09:26
#12 09. 12. 2011 09:46 — Editoval Rumburak (09. 12. 2011 09:58) Příspěvek uživatele Rumburak byl skryt uživatelem Rumburak. Důvod: Omyl
#13 09. 12. 2011 09:56
Re: Určete největší obsah lichoběžníku
↑ Rumburak:
Zdravím,
nechci se hádat, ale 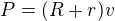 je opravdu obsah celého lichoběžníku (kyž v souladu s obrázkem je R polovina delší základny a r polovina kratší základny)
je opravdu obsah celého lichoběžníku (kyž v souladu s obrázkem je R polovina delší základny a r polovina kratší základny)
Offline
#17 09. 12. 2011 15:04
- Nanoliquid

- Příspěvky: 64
- Reputace: 0
Re: Určete největší obsah lichoběžníku
Děkuji mockrát za pomoc, ale nevím, jestli mi to pomůže, jelikož bych měl nejspíš využít metod pro vyšetřování průběhu funkce. Jenže nevím jak:(
Offline
#18 09. 12. 2011 15:10 — Editoval Rumburak (09. 12. 2011 15:11)
Re: Určete největší obsah lichoběžníku
↑ Nanoliquid:
Ahoj. Zkus začít tím, že si (znovu) přečteš můj příspěvek ↑ Rumburak: a odvodíš si předpis pro příslušnou funkci .
Podívej se také na příspěvek od koledgy: ↑ vanok:
Offline
#19 09. 12. 2011 15:23
- Nanoliquid

- Příspěvky: 64
- Reputace: 0
Re: Určete největší obsah lichoběžníku
Hledám tedy proměnnou y, pro kterou je maximální výška ?
Offline
#20 09. 12. 2011 16:01 — Editoval Rumburak (09. 12. 2011 16:04)
Re: Určete největší obsah lichoběžníku
↑ Nanoliquid:
Snad to myslíš dobře, ale nenapsal jsi to dobře. Podívej se na obrázek kolegy ↑ Cheop:, z něho budu nyní vycházet.
Z něho by Ti mělo být zřejmé, že každý z přípustných lichoběžníků, mezi nimiž hledáme ten s největším obsahem, má nějakou výšku 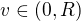
a tímto číslem je sám jednoznačně určen. To bude proměnná naší funkce S(v) pro výpočet obsahu libovolného takového lichoběžníka (já ve svém
odkazovaném příspěvku tuto proměnnou označil  ) .
) .
Body C[?, v], D[?, v] leží na kružnici o rovnici 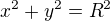 a z ní můžeme vyjádřit jejich x-ové souřadnice c, d tak, aby C=[c, v], D=[d, v] .
a z ní můžeme vyjádřit jejich x-ové souřadnice c, d tak, aby C=[c, v], D=[d, v] .
Je zřejmě , že 0 < c < R, d = -c . Nalézt funkční vyjádření c = c(v) a následně S= S(v) pro ten obsah už nechám na Tobě. Na tuto funkci pak
použiješ metody pro hledání extrémů.
Jak naznačuje ↑ vanok: , bude možno zavést substituci v = R sin t , 0 < t < pi/2 , (a tedy c = R cos t), což úlohu poněkud
usnadní.
Offline
#21 09. 12. 2011 19:56
Re: Určete největší obsah lichoběžníku
↑ Nanoliquid:
Tak tedy velká nápověda:
V mém obrázku máš všechny potřebné délky vyjádřené pomocí zakótovaného úhlu alfa. (a po jejich dosazení i vztah pro plochu lichoběžníka)
Ty máš vyřešit úlohu kdy je plocha lichoběžníku maximální. To se dělá (jak jistě víš) tak, že vztah pro plochu zderivuješ (proměnnou, podle které budeš derivovat je ten úhel alfa) a tuto dervaci položíš rovnu 0. Tím vypočítáš pro jakou hodnotu té příslušné proměnné (alfa) nabývá funkce (plocha lichoběžníku) extrému. (zde to bude samozřejmě maximum, protože minimum by jistě nastalo pro alfa=90stupňů) (V rámci korektnosti by to chtělo udělat i druhou derivaci a po dodasení vypočítané hodnoty z první derivace se přesvědčit, že se jedná opravdu o maximum (<0))
No a potom zpětně dosadíš vypočítanou hdnotu (alfa) do vztahu pro plochu. (i když po tobě se chce abys vypočítal strany licoběžníka - tak tedy dosadíš do vztahu pro r (c/2) a pak si odvodíš i vztah pro stranu b=d)
Offline
#22 09. 12. 2011 20:44
- Nanoliquid

- Příspěvky: 64
- Reputace: 0
Re: Určete největší obsah lichoběžníku
Mám tedy vztah 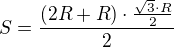 , Ta to mám vyjádřit pomocí úhlu alfa a poté zderivovat ??
, Ta to mám vyjádřit pomocí úhlu alfa a poté zderivovat ??
Offline
#23 09. 12. 2011 21:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Určete největší obsah lichoběžníku
↑ Nanoliquid:
Problém tohoto tématu je přemíra aktivity odpovídajících a minimální reakce autora dotazu, také se cestou podařilo různě přeznačit 4 vrcholy lichoběžníku.
Tvůj vzorec pro výpočet obsahu: 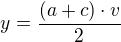
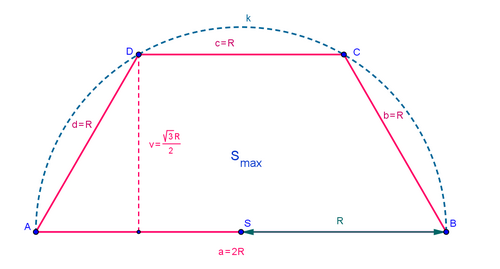
Obrázek od kolegy Honzce:
A Tvůj cíl je nahradit písmenka ve vzorci pro obsah (
 ,
,  ,
,  ) tak, aby ve vzorci bylo jen
) tak, aby ve vzorci bylo jen  ,
, 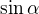 ,
,  . Je tento cíl jasný? Děkuji.
. Je tento cíl jasný? Děkuji.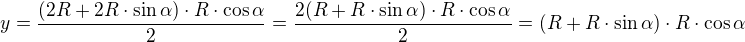
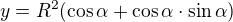
derivace (R je konstanta)

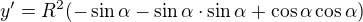
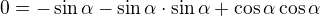
Offline
#24 09. 12. 2011 21:13
- Nanoliquid

- Příspěvky: 64
- Reputace: 0
Re: Určete největší obsah lichoběžníku
Snad je to jasné .... Máte pravdu, já už jsem z toho všeho celkem dosti zmatený.
Offline
#25 09. 12. 2011 21:16
- Nanoliquid

- Příspěvky: 64
- Reputace: 0
Re: Určete největší obsah lichoběžníku
Takže  Je to správně ?? a proměnnou je teda
Je to správně ?? a proměnnou je teda  ?? Děkuji mockrát
?? Děkuji mockrát
Offline
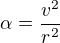 ??
??