Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 05. 08. 2008 01:16
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Made in Bulgaria
Minulý týden jsem měl tu čest se účastnit jedné takové matematické akcičky v Bulharsku. A něco málo jsem vám přivezl:
1) Najděte všechny spojité funkce f z R do R, pro které je f(x)-f(y) racionální, pokud je x-y racionální.
2) Mějme funkci f, která každému polynomu P přiřadí reálné číslo a platí, že pokud f(PQ)=0, pak f(P)=0 nebo f(Q)=0. Dokažte, že existují konstanty a,b takové, že pro všechny polynomy P je f(P)=a*P(b).
3) Nech? a_1,a_2,...,a_k je k různých nenulových celých čísel a P polynom s reálnými koeficienty.
a) Dokažte, že existuje a takové, že
P(a_i) dělí P(a) pro všechna i od 1 do k.
b) rozhodněte, zda pro každý polynom P existuje a takové, že
P(a_1)*P(a_2) dělí P(a).
4) Trojici čísel x,y,z nazveme pěknou, pokud x+y+z=1. Trojice a,b,c je "lepší" než trojice x,y,z, pokud je větší její medián. Najděte nejmenší n takové, že existuje množina S obsahující n pěkných trojic s následující vlastností: pro libovolnou pěknou trojici t je v S trojice v, která je lepší než t.
5) Rozhodněte zda existuje taková grupa G a její normální podgrupa H, že H má více automorfizmů než G.
6) Pro permutaci f na množině {1,..., n} definujeme d(f) jako součet
|1-f(1)|+|2-f(2)|+...+|n-f(n)|.
Označme Q(n,r) počet permutací f nad {1,...,n}, pro které d(f)=r.
Ukažte, že Q(n,r) je pro d>=2n sudé číslo.
7) Víme, že polynom x^(2k)-x^k+1 dělí x^(2n)+x^n+1. Dokažte, že
x^(2k)+x^k+1 dělí x^(2n)+x^n+1.
8) Dvě elipsy mají společné ohnisko. Dokažte, že se protínají nejvýše ve dvou bodech.
9) Dokažte, že  je dělitelné
je dělitelné 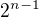 .
.
10) Polynom P(x) s celočíselnými koeficienty má 81 celočíselných kořenů. Ukažte, že pokud existují polynomy F(x), G(x) s celočíselnými koeficienty takové, že P(x)-2008=F(x)G(x), pak F i G mají stupeň alespoň 6.
11) Matice A je čtvercová a má tu vlastnost, že její prvek  je 0, pokud je i+j složené a 1, pokud je i+j prvočíslo. Ukažte, že determinant matice je druhá mocnina přirozeného čísla.
je 0, pokud je i+j složené a 1, pokud je i+j prvočíslo. Ukažte, že determinant matice je druhá mocnina přirozeného čísla.
12) V Hilbertovském prostoru nekonečné dimenze je dána ne nutně spočetná množina bodů S, každé dva ve vzdálenosti d. Dokažte, že existuje bod y z tohoto prostoru takový, že
je ortonormální systém vektorů.
Pokud by vás zajímalo více, pak navštivte
http://www.mathlinks.ro/index.php?f=79
případně oficiální stránky
http://www.imc-math.org
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#2 25. 08. 2008 21:13
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Made in Bulgaria
10) To snad nejde ukázat. 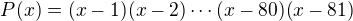 má celočíselné koeficienty a 81 celočíselných kořenů. Polynomy
má celočíselné koeficienty a 81 celočíselných kořenů. Polynomy
mají celočíselné koeficienty a platí P(x)=F(x)G(x). Přitom ale G(x) má stupeň pouze 1.
Offline
#3 25. 08. 2008 22:39
Re: Made in Bulgaria
V té jedničce to znamená, že f(x) - f(y) je racionální tehdy a jen tehdy, když je racionální x - y, nebo to je jen tak, že když je x - y racionální, tak je i f(x) - f(y) racionální?
Offline
#4 25. 08. 2008 22:50
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Made in Bulgaria
↑ BrozekP:Samozřejmě, vypadlo mi tam to "2008". Teď už to dokázat jde :)
↑ Olin:Druhá možnost je správně. (Výsledky ale pro obě možnosti jsou stejné a obtížnost řešení srovnatelná).
BRKOS - matematický korespondenční seminář pro střední školy
Offline
#5 25. 08. 2008 22:57
Re: Made in Bulgaria
Tak pokud všechny… Nejprve mě samozřejmě napadly lineární funkce s racionálním koeficientem u x, pak dále jsou to určitě všechny funkce 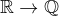 (libovolně divoké), pak k těmto funkcím můžeme přičíst výše uvedené lineární… No je toho hafo.
(libovolně divoké), pak k těmto funkcím můžeme přičíst výše uvedené lineární… No je toho hafo.
Offline
#6 25. 08. 2008 23:26
- Kondr

- Veterán
- Místo: Linz, Österreich
- Příspěvky: 4246
- Škola: FI MU 2013
- Pozice: Vývojář, JKU
- Reputace: 38
Re: Made in Bulgaria
↑ Olin:Máš pravdu, pokud vynecháme požadavek spojitosti, pak to bude mít spoustu divokých řešení (slovo spojité jsem doplnil).
BRKOS - matematický korespondenční seminář pro střední školy
Offline