Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 15. 10. 2011 17:50
Určení čísla N
Dobrý den, narazil jsem na příklad, u kterého si nevím rady. Vlastně ani moc nechápu to zadání, pokud by mi byl někdo ochotný pomoci, jak postupovat či něco podobného, budu jenom rád.
Určete nejmenší možné číslo N tak, že už není možné rozměnit 1 dolar na přesně N mincí. Můžete použít půldolary (50 centů), čtvrtdolary (25 centů), deseticenty, pěticenty a centy.
Offline
#2 15. 10. 2011 18:11 — Editoval Pavel Brožek (15. 10. 2011 18:12)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Určení čísla N
↑ Tue09:
Máme určit nejmenší. Tak začněme od toho nejmenšího N=2 (kdyby N=1, tak to nebude rozměnění) a postupujme k vyšším.
N=2: Dolar lze rozměnit na dva půldolary (to jsou dvě mince).
N=3: Dolar lze rozměnit na půldolar a dva čtvrtdolary (to jsou tři mince).
N=4: Dolar lze rozměnit na čtyři čtvrtdolary (to jsou čtyři mince).
...
U jakého N už nebude možné dolar rozměnit na N mincí? To je otázka.
Offline
#3 15. 10. 2011 21:16
Re: Určení čísla N
Děkuji moc. Už u toho sedím ale jakou dobu, jsem u čísla 15 a s vidinou toho, že bych to musel počítat číslo po číslu až do zítra mě moc neláká. Není na to nějaký rychlý postup, který to číslo určí nějak rychleji nebo ten dolar těmi mincemi N poskládám rychleji?
Offline
#4 15. 10. 2011 22:30
- halogan

- Ondřej
- Místo: UK
- Příspěvky: 4528
- Škola: IES FSV UK (09-12, Bc.)
- Pozice: student
- Reputace: 106
Re: Určení čísla N
Tak ono se to dá trochu zrychlit, když si šikovně vyberete mince, které se dají dobře dělit. Např.:
(předpokládejme, že prvních 9 jste ošetřil.)
Jeden dolar je 10 deseticentů. Když postupně budu dělit deseticenty na dva pěticenty, bude mi vždy jeden přibývat. Tak se dostanu na N = 20.
Teď vemu 9 deseticentů a ten desátý rozměním na 10 centovek. Mám 19 mincí a postupně jako předtím dělím ty deseticenty. Jsem na N = 28.
8 deseticentů a 20 centovek, dostávám se na 36.
30 centovek a 7 deseticentů, jsem na 44.
Teď nějak poskládat 45 mincí a můžeme jít dál.
Offline
#5 16. 10. 2011 13:37
Re: Určení čísla N
Děkuji. Vím že to asi není účelem toho příkladu, ale nevěděli byste někdo výsledek už prosím? Rád bych se posunul dál, ale to, že nebudu vědět výsledek mě bude znepokojovat a moc času na počítání jednoho a toho samého příkladu také nemám. Děkuji.
Offline
#6 16. 10. 2011 14:29 — Editoval vanok (16. 10. 2011 23:56)
Re: Určení čísla N
Tento zaujimavy problem mi pripomenul tento vseobecnejsi problem:
Dokazte ze ak 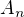 je pocet rieseni Diophantickej rovnice
je pocet rieseni Diophantickej rovnice  v
v 
potom nekonecna rada  je representovana rationalnov funkciov zo
je representovana rationalnov funkciov zo 
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 20. 10. 2011 11:06 — Editoval vanok (23. 10. 2011 13:06)
Re: Určení čísla N
↑ vanok: Tak maly navrat k problemu
Ako sa da jednoducho zistit 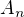 ?
?
Je iste viac metod.
Ja vam tu dam jednu: Je to coficient z 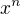 v tomto sucine
v tomto sucine *
* *
* *
* *
*
Vsimnite si ako je vytvoreny tento sucin
V prvej zatvorke sa mocniny z x su 0, 1, 2, 3, 4 ( aritmeticka postupnost z diferenciou 1) a tak ide o geometricku radu ktore ma sumu 
V druhej su 0, 5, 10, ...
Ze je to vam jasne teraz.
Formalne tento sucin je :

a je jasne ze jej rozvoj  nam da vsetki
nam da vsetki 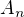
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 23. 10. 2011 12:51 — Editoval vanok (23. 10. 2011 13:03)
Re: Určení čísla N
↑ vanok:
Ako som slubil, davam tu priklad ako konkretne nast 
Z tohto sucinu staci zobrat v kazdom faktory "odrezat " sumy tak ze sa 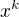 pre
pre  jednoducho ignoruju vsetki take monomy
jednoducho ignoruju vsetki take monomy




Tak staci len nast coeficient z  v sucine
v sucine





v tomto sucine PLATNE COEFICINTY SU LEN pre k= 1; 2,..., 14
a preto sa netreba namahat a pocitat koeficienty pre

Odpoved na otazku co kolko rieseni ma nasa rovnica pre n= 14, je 4: tak za uvedenych podmienok mozme "zaplatit"sumu 14 cts 4mi sposobmy
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 23. 10. 2011 20:41 — Editoval vanok (24. 10. 2011 17:49)
Re: Určení čísla N
Ahoj ↑ Tue09:, NIE CELKOM DOBRA NOVINKA
V mojom probleme  je 292, tak na riesenie tvojho problemu treba prestudovat najviac 292pripadov
je 292, tak na riesenie tvojho problemu treba prestudovat najviac 292pripadov
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 27. 10. 2011 14:01 — Editoval vanok (16. 12. 2011 00:27)
Re: Určení čísla N
↑ vanok:,
Ako som slubil pokracujem moje matematicke prechadzky na podobne tematiky
Zda sa mi ze Sierpincki polozit takuto ulohu
Najdite najvadcie prirodzene n pre ktore nema rovnica
 ,
, 
riesenie.
Som isty ze niekto to tu vyriesi.
edit oprava preklepu
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#11 29. 10. 2011 20:17 — Editoval miso16211 (29. 10. 2011 20:19)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: Určení čísla N
šak 100 centy, dollar rozdelim na 100 centiki - 100 minci, či mince sa nemôžu opakovať?
a najmenšie je 2 či 100 ?
Offline
#12 29. 10. 2011 22:21
Re: Určení čísla N
Ahoj ↑ miso16211:,
Asi si precital trochu nepozorne problem od↑ Tue09:, ide o to aby sa naslo take najmensie mozne cislo N (pocet minci) ze je nemozne rozmenit 100cts pomocou dovolenych minci.
Inac som tu navyse riesil trochu iny problem ↑ vanok: ... ktory je tiez zaujimavy, a v niecom sa pripomina povodny problem.
A posledny problem sa tyka podobnej tematiky je ↑ vanok: ktory tu coskoro vyriesil, le kazdy moze nan dat svoje riesenie.
Srdecne Vanok
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#13 12. 12. 2011 13:23 — Editoval vanok (16. 12. 2011 00:26)
Re: Určení čísla N
↑ vanok:,
Tento problem stale caka na riesenie:
Najdite najvadcie prirodzene n pre ktore nema rovnica ,
, 
riesenie.
Indikacia
Najprv studujte tri pripady
a)  ,
,  a
a 
b)  ,
,  a
a 
c)  ,
, 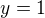 a
a 
Niekoho to inspiruje?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#14 13. 12. 2011 09:40
Re: Určení čísla N
Offline
#15 13. 12. 2011 11:05
Re: Určení čísla N
↑ standyk:,
V tomto priklade 
Ale sa nedivim lebo ak citas aj inojazycne knihy pojem prirodzeneho cisla sa meni podla narodnosti.
Mozno by bolo treba urobit tabulku podla zvyklosti.
Podobny problem je aj zo slovamy kladny. Podla jazyka ide o ostru alebo neostru nerovnost...
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 13. 12. 2011 11:21
Re: Určení čísla N
↑ standyk:
Ano x, y nenulove niesenia.
Teraz iste pochopis moj navod na 100%.
Som rad ze sa zaujimas o taketo problemy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 13. 12. 2011 11:50
Re: Určení čísla N
↑ standyk:,
prave ze existuje ... skus najst pre 30 napriklad
pozri na moj navod: (a)
Vidim ze sa z tym trochu pobavis.
Musim teraz ist vecer odpoviem ak nenajdes dokonale riesenie!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 16. 12. 2011 00:25
Re: Určení čísla N
Najdite najvadcie prirodzene n pre ktore nema rovnica

riesenie.
RIESENIE
Najprv studujme tri pripady
a)  ,
,  a
a  , mame
, mame 
b)  ,
,  a
a  , mame
, mame 
c)  ,
, 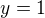 a
a  , mame
, mame 
To znamena ze rovnica  ma riesenie pre
ma riesenie pre  .
.
Akoze



Pre n=1, 2, 3, 4, 5, 6, 7 nasa rovnica nema riesenie.
Pre n = 9, musi 3|5y a tak 3|y co znamena 15|5y a n=3x+ 5y>15, co je nemozne.
Toto plati aj pre n=12 a n=15.
A na koniec, pre n=10 musi 5|3x, a tak 5|x a z toho 15|3x a 15|n=3x+ 5y>15, co je nemozne.
dosledok:Najvadcie n, pre ktore nema rovnica 
 riesenie je
riesenie je
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
![kopírovat do textarea $ k \in [2;...;100]$](/mathtex/4c/4c7df7e976346328e5243a43fab1d01f.gif) take ze
take ze  .
.  bude riešenie
bude riešenie ![kopírovat do textarea $[5,0]$](/mathtex/2f/2f9b5974511e95c356d1fe3bdf62959b.gif)
 ak
ak 