Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 13. 12. 2011 18:48
Re: rovnice s x^3
Ahoj, příklad můžeme řešit užitím Cardanových vzorců (http://cs.wikipedia.org/wiki/Cardanovy_vzorce), nebo jeden kořen tipnout a polynom  pak vydělit polynomem
pak vydělit polynomem  , kde x_0 je kořen rovnice. Získáme kvadratickou rovnici a tu jednoduše vyřešíme.
, kde x_0 je kořen rovnice. Získáme kvadratickou rovnici a tu jednoduše vyřešíme.
Jsem omylný, proto ne vše, co jsem napsal, je zaručeně správně.
468
Offline
#3 13. 12. 2011 18:52
Re: rovnice s x^3
↑ TomDlask:
Tenhle odkaz je i pro mne dost nepraktický, natož pro kolegu.
1) Není to náhodou takhle : ?
Volané číslo je imaginární. Otočte prosím telefon o 90 stupňů a zkuste to znovu.
Offline
#4 13. 12. 2011 19:10
Re: rovnice s x^3
Alivendes napsal(a):
↑ TomDlask:
Tenhle odkaz je i pro mne dost nepraktický, natož pro kolegu.
1) Není to náhodou takhle : ?
ne ne ne ale kouknul jsem se teda na to znovu a mel jsem tam drobne chyby za ktere se opravdu omlouvam 
Offline
#5 13. 12. 2011 19:11
Re: rovnice s x^3
↑ Alivendes:
Ano, Cardanovy vzorce jsou celkem obtížné na užití... napadá mne ještě metoda tečen, ta by mohla být jednodušší.
Jsem omylný, proto ne vše, co jsem napsal, je zaručeně správně.
468
Offline
#6 13. 12. 2011 19:16
#8 13. 12. 2011 19:53
Re: rovnice s x^3
↑ TomDlask:
Nevim jak odpovedet :-D co dokazu spocitat ? to co umim. co nedokazu ? to co neumim, opravdu nevim jak ti mam na tuhle otazu odpovedet tohle je btw priklad z VS teda je to spektralni rozklad a pri vypoctu determinantu jsem se dostal sem a potrebuju vypocitat 3  abych mohl pokracovat
abych mohl pokracovat
Offline
#9 13. 12. 2011 20:06 — Editoval TomDlask (13. 12. 2011 20:07)
Re: rovnice s x^3
Pro získání přibližných kořenů se může hodit metoda půlení intervalu. Podle grafu odhadneme, že jedno řešení bude mezi čísly (např.) 4 a 7, protože f(4)<0 a f(7)>0 (mezi nimi musí být nějaké f(x)=0), zkusíme 5,5 (leží mezi 4 a 7).
f(5,5) je větší než 0 takže řešení je mezi 4 a 5,5. Zkusíme 4,75 (leží mezi 4 a 5,5).
f(4,75) je menší než 0 takže řešení je mezi 4,75 a 5,5. Zkusíme 5,125.
f(5,125) je menší než 0 takže řešení je mezi 5,125 a 5,5
A tak dále - dokud nebude dostatečná přesnost
edit: beru 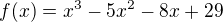
Jsem omylný, proto ne vše, co jsem napsal, je zaručeně správně.
468
Offline
#11 13. 12. 2011 22:56
Re: rovnice s x^3
tOree napsal(a):
↑ TomDlask:
co dokazu spocitat ? to co umim. co nedokazu ? to co neumim
Tak to bývá.
tOree napsal(a):
tohle je btw priklad z VS teda je to spektralni rozklad a pri vypoctu determinantu jsem se dostal sem a potrebuju vypocitat 3
abych mohl pokracovat
Tak se podívej do sekce VŠ, kde si přečti druhé zvýrazněné téma "LA pro VŠB", nebo tak nějak. Jistě se ti bude líbít. Kolegové se hezky snaží dát ti numerické řešení, ale to ti bude k ničemu. Jednak proto, že ty potřebuješ vlastní čísla přesně, jednak proto, že jsi téměř určitě už při výpočtu char. polynomu udělal chybu - nikdo by vám snad nezadal příklad, kde vychází takové zhovadilosti jako tady. Pošli celý svůj postup.
↑ TTresh:
Než to opsat z Wolframu, bylo by bývalo lepší sem dát odkaz. Sice bys pak nevypadal tak chytře, ale na druhou stranu kolega by příště možná zkusil konzultovat nástroje sám. Ačkoli vzhledem k tomu, že si nedělá starosti ani se správným opisem zadání, umístěním do správné sekce, ani se neobtěžuje s interpunkcí je to možná přehnaně optimistický předpoklad. Ale nikdy nevíme.
Offline
#13 14. 12. 2011 00:28
Re: rovnice s x^3
↑ tOree:,
nieco nesedi!
ak ten polynom ma ti dat vlastne hodnoty tvojej matice tak to je nemozne
Stopa tvojej matice je 7 ( a vieme ze to je tiez sucet vlastnych hodnot matice)
a podla polynomu sucet vlastnych cisiel je 5
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 14. 12. 2011 00:37
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: rovnice s x^3
↑ tOree:
Pokud jsou všechny kořeny celá čísla, pak každý kořen dělí koeficient d. To je jednoduše vidět z Vietových vzorců. Ve škole se pak obvykle zadávají takové matice, že vlastní čísla jsou celá čísla.
Offline
#18 14. 12. 2011 01:03 — Editoval vanok (14. 12. 2011 01:08)
Re: rovnice s x^3
↑ tOree:,
nemozne pre tuto maticu:
1 -3 -1
-3 1 1
-1 1 5
lebo ↑ vanok:
A je aj uzitocne i toto asimilovat:
http://en.wikipedia.org/wiki/Trace_%28l … r_operator
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#19 14. 12. 2011 01:05
Re: rovnice s x^3
↑ LukasM: dekuji za odkaz ktery mi pomohl pro vypocet co se tyce v sekce nechtel jsem to davat do VS protoze jsem si rekl ze tohle se bere i na strednik skolach spletl jsem se zadani jsem pocital a neopisoval z "wolframu" nebo jak si to myslel u interpunkce mno na klavesnici jsem se naucil psat bez ni vzhledem k tomu ze se pohybuju jen na EN klavesnici.
dekuji vsem za pomoc
Offline
#20 14. 12. 2011 01:14
Re: rovnice s x^3
vanok napsal(a):
↑ tOree:,
nemozne pre tuto maticu:
1 -3 -1
-3 1 1
-1 1 5
lebo ↑ vanok:
A je aj uzitocne i toto asimilovat:
http://en.wikipedia.org/wiki/Trace_%28l … r_operator
Asi nejsem schopny vyresit malou nasobilku... :-D
Offline
#24 14. 12. 2011 09:39
Re: rovnice s x^3
↑ tOree:
Do wolframu stačí zadat tu matici a dostaneš přímo charakteristický polynom, takže je zbytečné je sem posílat a ptát se jestli jsou dobře.
Jinak lambdy nemusí vyjít jako celá čísla, i když to tak často bývá, jak říká ↑ Pavel Brožek:. Ale neradil bych na to spoléhat, a kontrolovat si podle toho výpočet.
Předpokládám, že jsi z VŠB, tak se rovnou na něco zeptám. Za prvé, učili vás tam Laplaceův rozvoj? Pokud ano, tak si při výpočtu char. polynomu nejdřív přičti druhý sloupec k prvnímu, a pak odečti první řádek od druhého. A hle, rázem nepočítáme rovnici třetího stupně (což se nám líbí, nemusíme hádat kořeny), ale jen druhého. Tím se krásně řeší ten "problem toho ze nedokazu vypocitat rovnici ax^3+bx^2+cx+d=0" - ale už jsem tohle kdysi radil jednomu tvému kolegovi, který to vůbec neocenil, a radši zůstal u správné char. rovnice, kterou ovšem neuměl vyřešit.
Za druhé, učili vás tam, že pokud o něčem naprosto nic nevíte, je lepší začít úkoly dělat dřív než 20 hodin před termínem? Je to totiž společná vlastnost snad všech expertů na spektrální rozklad od vás.. A i když je mi jasné, že když teď uděláš dojemnou scénu, někdo ti sem pošle celé řešení, vůbec si to nezasloužíš.
Offline
#25 14. 12. 2011 10:25
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: rovnice s x^3
LukasM napsal(a):
když teď uděláš dojemnou scénu, někdo ti sem pošle celé řešení
:-) vrcholem mého snážení bylo druhé úvodní téma sekce VŠ, doufám, že jsem dostatečně zdůraznila Laplaceův rozvoj a pokyn "začínat včas" (jsem ochotna i nadále to téma vylepšovat, ale to je tak všechno).
Zdravím.
Offline
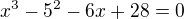 tak nejak nevim jak na to diky predem :-))
tak nejak nevim jak na to diky predem :-))