Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limit posl., lim. fnc., integral... (TOTO TÉMA JE VYŘEŠENÉ)
#2 26. 08. 2008 13:50
Re: Limit posl., lim. fnc., integral...
Offline
#3 26. 08. 2008 14:27
Re: Limit posl., lim. fnc., integral...
Myslím, že včera jsi dostal velkou dávku postupů a řešení; je na čase aktivně se participovat a nejprve uvést své myšlenky k řešení, nebo dokonce celá řešení (můžou být i chybná - opravíme).
Nevidím další smysl řešit tvé úlohy. To si můžeš klidně někoho zaplatit, a? ti to vyřeší. Tady na fóru se ti budeme snažit pomáhat především pochopit souvislosti. Význam matematiky na školách není jen v aplikacích matematiky. Její význam na výchovu člověka je daleko hlubší (zpravidla není patrný studentům a někdy dokonce i vyučujícím - takový uživatel Pavel na tomto fóru by mohl vyprávět podobně jako já).
Offline
#4 26. 08. 2008 16:42
Re: Limit posl., lim. fnc., integral...
dobrá chápu..ale jak bych to řekl jsem chudej student:D ale apson jeslti mi to vzdy skontrolujete jeslti pocitam spravne budu rad:) zatim sem vypocital první dva příklady... http://forum.matweb.cz/upload/828-20_1_2.JPG
Offline
#6 26. 08. 2008 17:34
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limit posl., lim. fnc., integral...
↑ emko02:
Výsledky jsou určitě dobře. Na začátku třetího řádku ve jmenovateli jmenovatele má být ale 2 (ne n) a v dalším výrazu na tomtéž řádku má být v exponentu v jednom jmenovateli 2 (ne n). Ale dokončil jsi to správně, tak předpokládam, že si to asi jen špatně napsal.
Offline
#7 26. 08. 2008 19:14
Re: Limit posl., lim. fnc., integral...
tak ja sem na tohle tema budu hazet svoje řešeny priklady:) tady mam par.. http://forum.matweb.cz/upload/216-12_124.JPG u toho druhyho prikladu to lnsinx/x je vysledek a tady je pokračovaní toho 4 http://forum.matweb.cz/upload/544-12_124_b.JPG
Offline
#9 26. 08. 2008 21:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
↑ emko02:
4) začátek je dobře, rozklad na parciální zlomek není dobře:
dělení mnohočlenu mnohočlenem (přičtení - odečtení v čitateli, jak používaš, je možné):
(x^4 - 3):(x^3+x^2) = x-1
-
x^4+x^3
________
-x^3-3
-
-x^3 -x^2
------------
x^2-3
máme integrovát:
Zlomek  máme rozložit na parciální zlomky:
máme rozložit na parciální zlomky:

A+C =1
A+B =0
B=-3, odsud A =3, C = -2
dosazení mezí a vypočet určitého integralu asi nebude problém.
Doufám, že jsem to nějak nepopletla :-)
OK?
Offline
#11 27. 08. 2008 17:27 — Editoval jelena (27. 08. 2008 17:27)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
↑ emko02:
Zdravím :-)
v některém z předchozích příspěvků jsem dávala odkaz na www.mojeskola.cz Opravdu hodně pomůže - http://www.mojeskola.cz/Vyuka/Php/
Meze se dosazuji tak, že jedřiv za x dosadím horní mez (zde číslo 2) - stejný výraz, ve kterém za x dosadím dolní mez (zde číslo 1) - nechávám i včetně absolutních hodnot, nemusí tam, samozřejmě být, jen aby bylo videt, že jsem jen nahradila x, nic víc. 
OK?
myslim, že odkaz na stranky pana Maříka už byl, ještě přidám můj standardní odkaz na wims
---------
Ještě k zadání 2 - napíš, co tam máš na závěr, ten náznak, co vídim na okraj papíru, se mi nezdá, děkuji.
Offline
#13 28. 08. 2008 13:37
Re: Limit posl., lim. fnc., integral...
tak sem hazim dalsi priklady myslim si ze jsou v poho jen bych potřeboval ujištění od vás těch chytrých:) mod diky:) jenom u toho integralu tady http://forum.matweb.cz/upload/289-bons023.jpg
nevim jak dal pokračovat:(
pak mam tady dalsi prikladky ty by meli bejt taky v poho http://forum.matweb.cz/upload/548-bons021.jpg a tady pokračovaní http://forum.matweb.cz/upload/356-bons022.jpg
v ty druhy derivaci u ty funkce asi bude nejakej priklik určo:D snad ne:P
Offline
#14 28. 08. 2008 17:28
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
↑ emko02:
Zdravím :-) výpočet limity z 2. zadání se mi nezdal a nadále nezdá. Podle toho, co vidim ve vašich výpočtech, máte na to nějaký "ustalený postup". Ja mám tento odvozený vzorec pro odstranění neurčitosti 1 * oo, ale zda ho také používáte, nevím.
Táto úprava se používá, pokud lim u(x) je 1, lim v(x) je oo, pro x -> x_0

Budu tedy hledát tuto limitu:

Už teď děkuji kolegům za spravedlivou kritiku :-)
Ještě přidám poznámky k výpočtům od kolegy bons.
Offline
#15 28. 08. 2008 18:08
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
↑ bons:
Zdravím :-)
od chytrých - to je silné slovo (možná od trochu více vycvičených :-)
Zadání 11. :
1) v pořádku
2) použitím l´Hospitala je dobře vytvořena limita zlomku 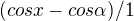 , po tomto kroku už dostavame limitu 0/1, ve vysledku má být 0
, po tomto kroku už dostavame limitu 0/1, ve vysledku má být 0
(proč je přeškrtnutí cos a?? - není to dobře).
3) začátek OK, pouze není uvedeno, proč parametr a byl změnen na číslo 3?
Dál se počítá s číslem 3, má to být dokončeno?
4) Začátek integrování OK, rozklad na parciální zlomky také.
Při hledání koeficientů (pokud se nepodaří "odmazání pomocí vhodného dosazování x) je možné použít porovnání koeficientů při stejných mocninách x
A = 1
A+B = 0, odsud B = -1, C = 0
je potřeba integrovat zlomky:
1/x - tabulkovy integral, vede na ln|x|
-x/(x^2+1), zde použit substituci x^2 = t, opět téměř tabulkový integral, ve výsledku bude (-ln(x^2+1))/2
test 32 - OK.
Kolegové od opravdových matematiků určitě budou mít poznámky k úpravě (i když ropzluštít ten text je celkem umění).
Hodně zdaru :-)
Offline
#16 28. 08. 2008 18:38
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limit posl., lim. fnc., integral...
↑ jelena:
Kde všechna ta pravidla na limity bereš :-)? Myslím, že kritika na tvůj příspěvek může být jedině pozitivní, zcela s postupem souhlasím :-). Zkusil jsem si ale to pravidlo dokázat, tak pokud by to někoho zajímalo, zde je můj pokus:
Předpokládám tedy, že pravidlo zní: Nech?  ,
, 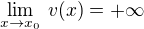 a
a  . Potom
. Potom  .
.

(nepovažujte to prosím jako korektní důkaz, neřeším moc existenci limit a diferencovatelnost funkcí :-)
Nemáš, Jeleno, náhodou odkaz na lepší důkaz?
Offline
#17 28. 08. 2008 19:18
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
↑ BrozekP:
Zdravím :-)
Bohužel, ja to mám nacvičeno od VŠ chemické v Moskvě a nějak si to udržuji, ae právě odvození vztahu - to si netroufám.
Z českých používám pouze Rektoryse a Jarníka, jinak je to vše v ruštině, hodně tady:
http://eqworld.ipmnet.ru/ru/library.htm a tak různě se koukám na Vychod :-)
Marián dával také odkaz na Demidoviče a Antidemidoviče v tomto tématu: http://forum.matweb.cz/viewtopic.php?id=172 - ale v těchto důkazech se těžko vyznám, jak tvrzení C vyplývá z tvrzení B na základě A - na to opravdu nemám :-)
Já se podívám, jestli tam je odvozen zrovna tento vztah - za chvilku.
Offline
#18 28. 08. 2008 20:01 — Editoval jelena (28. 08. 2008 20:02)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
↑ BrozekP:
V materialech od Mariana - slozka Antidemidovic - kniha Lyashko Tom 1 od str 79 originálu, konkterně tento vztah je na str. 80, ale vztahuje se k tomu i předchozí str.
Třeba tomu tvému důkazu rozumím :-) a děkuji moc za reakci.
Offline
#19 28. 08. 2008 20:05
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limit posl., lim. fnc., integral...
↑ jelena:
Bohužel azbuku přečtu velmi omezeně a rusky neumím, takže z ruského textu rozumím pouze slovům podobným těm českým/mezinárodním a vzorcům. Ale díky, třeba o antiděmidovičovi jsem vůbec nevěděl, ten se určitě bude hodit :-)
Offline
#20 28. 08. 2008 21:50 — Editoval BrozekP (30. 08. 2008 13:04)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limit posl., lim. fnc., integral...
↑ jelena:
Díky moc za ten přímý odkaz, ten důkaz tam je trochu elegantnější. Uvedu ho pro ostatní:
V druhé rovnosti byla využita limita 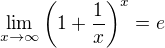 .
.
Offline
#21 28. 08. 2008 22:35 — Editoval Jorica (28. 08. 2008 22:36)
Re: Limit posl., lim. fnc., integral...
↑ BrozekP:
Hmmm, taky jsem se zaujetim koukala na uvedeny postup vypuctu tohoto typu limit.....taky jsem se s tim jeste nesetkala....a dukaz je opravdu elegantni ;-)
Jeleno, Vas zdravim ;-)
Offline
#22 28. 08. 2008 23:16
Re: Limit posl., lim. fnc., integral...
↑ Jorica:↑ BrozekP:
Já jsem se s tímto postupem seznamoval v úvodním cvičeni k matematické analýze v 1. semestru. Dokonce toto uvádím ve cvičení analýzy pro změnu nyní já. Popravdě řečeno, studenti nemají smysl pro krásné elegantní odvození nebo důkaz. Mají rádi hotové vzorce a to nemohu připustit a o vhodnosti takového laxního přístupu nejsem přesvědčen.
Offline
#23 28. 08. 2008 23:27
Re: Limit posl., lim. fnc., integral...
↑ Marian:
Opravdu vzpominam, vzpominam a mam pocit, ze tento obrat pri vypoctu limit mi byl dosud utajen, ale kdo vi, treba uz zapracovala skleroza ;-) A zkusenost se studenty mam podobnou....nejradeji jsou, kdyz maji "kucharku" :-( Tj. zadat typicky priklad, na ktery maji konkretni sled kroku, ktere vedou k vysledku. Jakykoliv jiny priklad, je podle jejich nazoru zakerny :-)
Offline
#24 29. 08. 2008 00:47
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limit posl., lim. fnc., integral...
Zdravím vás srdečně :-)
Kdyz vidim důkaz kolegy ↑ BrozekP:, tak bych si už dovedla představit i odvozování vzorce od druhé pozoruhodné limity.
Sama bych ale na důkaz určitě netroufla, těžko bych dokazala formulovat správná tvrzení :-) proto se nesmite zlobit, že jsem navrhla jen použití vzorce. Včera jsem nějakou dobu nad touto limitou stravila a porad se mi nezdal závěr postupu od autora dotazu, k začatku jsem původně výhrady neměla.
Myslím, že stejným způsobem se má řešit i další zadání (číslo 2) od kolegy. A řeší se to tedy odvozovaním, jak provedl kolega ↑ BrozekP: ? Jelikož ostatní úlohy z přiložených testů se mi zdaji zcela základní a jednoduché - a že se objevila tato limita?
↑ Jorica:
Pokud umí použit "kucharku" - to už je přece úspěch, víte, jak taková "Kuchařka pro začatečniky" má označení - minimální obtižnost až nejvyšší :-)
Offline
#25 29. 08. 2008 08:28 — Editoval kaja.marik (29. 08. 2008 11:03)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Limit posl., lim. fnc., integral...
↑ Marian:
asi proto, ze v tom odvozeni je takovy dost umely krok
mozna by to slo takto:
To prostredni je (az na oznaceni) Замечательный логарифмический предел a jde k jednicce
Sice tam je taky umely krok, ale to, ze se mam zbavit logaritmu (obecne ze se muzu v limite zbavit nejake hnusne funkce) pomoci polynomu, ktery roste stejne rychle, je takovy bezny obrat a vyuzije se casto. Mozna to i Jorica delala timto zpusobem vzdycky az v probehu vypoctu a neuvedomovala si, na jaky to vlastne vede vzorec :)
To s tim rafinovanym prevodem na mocniny je sice pekne, ale jestli to ma uspech zalezi na tom, jake je publikum. Na Karlovce to urcite oceni, na technikach asi ne :(
Offline
Stránky: 1 2
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Limit posl., lim. fnc., integral... (TOTO TÉMA JE VYŘEŠENÉ)
