Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#76 10. 08. 2008 17:55
Re: Limity
K tomuto:
matoxy napsal(a):
k príkladu č.93.)
len by som mal otázku k členom p a q. To, že člen p je počiatočná rýchlos? a q je počiatočná dráha by sme mohli zisti? tak, že by sme sledovali "správanie" paraboly pri dosadzovaní rôznych dôležitých čísel za členy p a q?
Už mi je to jasné.
- Graf funkcie s(t)''=2k, keďže funkcia je konštantná vyplíva z toho, že o "jej výške" rozhoduje iba písmenko k. Keďže je to graf zrýchlenia, tak k bude zrýchlenie.
- Graf funkcie s(t)'=2kt + p. O tom kde bude pretína? graf funkcie y-ovú os rozhodne písmenko p. Keďže je to graf okamžitej rýchlosti, tak o tom aká je rýchlos? v čase nula rozhoduje p.
- Graf funkcie s(t)=2kt^2 + p +q. V čase t=0 bude funkčná hodnota rovná q. Keďže je to graf dráhy podľa času, tak q bude počiatočná dráha.
K tomuto:
matoxy napsal(a):
96.) Zrýchlenie by išlo dopočíta? takto:
. Len sa mi na tom nepáči to, že tam vôbec netreba derivácie a nejak ma nenapadá ako by mi pri tom mohly pomôc?.
Uhm, len neveim prečo sa mi vtedy nejak nepozdávalo, že predpokladáme, že 2. derivácia dráhy je zrýchlenie, ale z grafu je to jasné a teda odvodenie toho vzorca už chápem. Čo sa týka odvodenie tohto vzorca pomocou integrácie, tak to asi nechám na pozdejšie.
A ruština u mňa zatiaľ nie, ani azbuku som sa ešte nenaučil, no tiež to patrí do kategórie časom:).
You know who
(or maybe not)
Offline
#77 10. 08. 2008 22:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Limity
↑ matoxy:
Jsou ještě malé drobné nesrovnalosti, ale to detail :-)
Graf funkce s''(t)=a (konstanta - zrychlení), nebudeme tam davat 2k, ale rovnou a jako označení pro zrychleni. Jinak celý tvůj výklad OK.
Graf funkce s´(t)=at + p - tady všechno OK
Graf funkce s(t)=(a/2)t^2 + pt +q - tady jsem to změnila, navazuje na použití a hned na počátku, dále u p se musí objevit t (pro kontrolu derivuj). A ted už jen doplnit, co jsi správně usoudil ohledně p, q.
Kroky, co jsi provedl od s''(t)=a až k s(t) je totez, jaku užití integralu pro odvození vzorce :-) - trochu lépe řečeno hledání primitivní funkce
Myslim, že už je to celé jasné :-)
Offline
#78 24. 08. 2008 18:29
Re: Limity
Po menšej-väčšej prestávke som ešte na chvíľu znova tu.
Rád by som ešte poradi? s pár príkladmi na vyšetrovanie priebehu funkcie, resp. hľadanie asymptot postupom aký je uvedený tu.
1.) Ak by som hľadal asymptotu ku funkcií 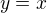 , vyšlo by mi, že je táto funkcia asymptotou samou sebe. Správne? Ak áno nie je to trocha zvláštne? Totiž v škole sme si asymptotu definovali ako dotyčnicu v nekončene a to sa mi pre takéto zistenie nehodí.
, vyšlo by mi, že je táto funkcia asymptotou samou sebe. Správne? Ak áno nie je to trocha zvláštne? Totiž v škole sme si asymptotu definovali ako dotyčnicu v nekončene a to sa mi pre takéto zistenie nehodí.
2.) Ak by som hľadal symptotu k funkcii  došiel by som k rovnici asymptoty:
došiel by som k rovnici asymptoty:  . Takáto rovnica existova? myslím nemôže nie? To by znamenalo, že funkcia nemá asymptotu, ale podľa postupu uvedeného na stránke je podmienka toho, či má funkcia asymptotu to, či existujú limity:
. Takáto rovnica existova? myslím nemôže nie? To by znamenalo, že funkcia nemá asymptotu, ale podľa postupu uvedeného na stránke je podmienka toho, či má funkcia asymptotu to, či existujú limity:  a
a ![kopírovat do textarea $b=\lim_{x \to +\infty}[f_{(x)}-ax]$](/mathtex/a3/a31727cf6ebdeca604853bc9f8c2f540.gif) . Ak sa nemýlim tak obidve z týchto limít existujú. A funkcia napriek tomu nemá asymptotu. Kde je chyba v tomto postupe?
. Ak sa nemýlim tak obidve z týchto limít existujú. A funkcia napriek tomu nemá asymptotu. Kde je chyba v tomto postupe?
You know who
(or maybe not)
Offline
#79 24. 08. 2008 18:58
Re: Limity
↑ matoxy:
ad 2. Pokud vypoctes , pro funkci
, pro funkci  , je vysledkem nekonecno, tzn. ze limita existuje, ale jde o limitu nevlastni. Mylsim, ze by melo byt v textu presneji uvedeno, ze fce ma asymptotu se smernici, jejiz rovnice je
, je vysledkem nekonecno, tzn. ze limita existuje, ale jde o limitu nevlastni. Mylsim, ze by melo byt v textu presneji uvedeno, ze fce ma asymptotu se smernici, jejiz rovnice je  , pokud existuje VLASTNI limity pro a, b.....
, pokud existuje VLASTNI limity pro a, b.....
Podle tohoto upresneneho tvrzeni fce  asymptotu se smernici nema, protoze vysledkem limity pro koeficient a (pro x jdouci k +oo i -oo) je oo.
asymptotu se smernici nema, protoze vysledkem limity pro koeficient a (pro x jdouci k +oo i -oo) je oo.
Offline
#80 24. 08. 2008 19:00 — Editoval Pavel (24. 08. 2008 19:01)
Re: Limity
↑ matoxy:
ad 1) No ano, funkce y=x je sama sobě tečnou v libovolném reálném čísle. Definujeme-li asymptotu o rovnici 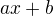 funkce f(x) v
funkce f(x) v 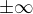 pomocí limity
pomocí limity  , pak je tato podmínka pro funkci f(x)=x a asymptotu y=x splněna.
, pak je tato podmínka pro funkci f(x)=x a asymptotu y=x splněna.
ad 2) Obě limity existovat musí, ale navíc, tyto musí být vlastní. Což pro první z nich neplatí.
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#83 24. 08. 2008 20:53
Re: Limity
↑ matoxy:
Laicky řečeno, Marian mi odpustí zjednodušení :-), pokud se v zadání objeví sinus, cosinus, tangens nebo cotangens, "zavání" to periodičností. Pak je třeba hledat minimální kladné p takové, že f(x+p)=f(x).
Backslash je v TeXu tak důležitý jako nekonečno při dělení nulou v tělesech charakteristiky 0.
Offline
#84 25. 08. 2008 06:52 — Editoval Marian (25. 08. 2008 07:23)
Re: Limity
↑ Jorica:↑ Pavel:↑ matoxy:
Zdravím Vás, Pavla pak obzvláště.
Chtěl bych ještě cosi dodat. Pokud není nijak zřetelné nebo není uvedeno, není vůbec zřejmé, co značí symbol  . V některých textech značí toto výhradně
. V některých textech značí toto výhradně  , v jiných je uvedena poznámka o tom, že má smysl
, v jiných je uvedena poznámka o tom, že má smysl 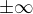 , což jsou již dva symboly. Tedy ve výrazu
, což jsou již dva symboly. Tedy ve výrazu  jsou ukryty dvě limity. Musí existovat alespoň jedna z nich a být vlastní. K tomu, aby existovala asymptota (nesvislá), je zapotřebí ještě spočítat nebo jinak ukázat, že existuje příslušná limita
jsou ukryty dvě limity. Musí existovat alespoň jedna z nich a být vlastní. K tomu, aby existovala asymptota (nesvislá), je zapotřebí ještě spočítat nebo jinak ukázat, že existuje příslušná limita  . Celkem se tedy de facto počítají limity čtyři.
. Celkem se tedy de facto počítají limity čtyři.
A maličká poznámka k Pavlovi a jeho periodicitě. Funkce f(x) se nazývá periodická, jestliže pro všechna  existuje fixní číslo [/tex]p>0[/tex] takové, že platí rovnice
existuje fixní číslo [/tex]p>0[/tex] takové, že platí rovnice  . Pak číslo p>0 nazýváme periodou funkce f(x) na D_f. Číslo se pak nazývá minimální perioda funkce f(x) na D_f.
. Pak číslo p>0 nazýváme periodou funkce f(x) na D_f. Číslo se pak nazývá minimální perioda funkce f(x) na D_f.
Tedy stačí ukázat, že takové číslo existuje, není nutné hledat nejmenší.
Příklad. Funkce  je jistě periodická s
je jistě periodická s  , ale funkce
, ale funkce  už periodická není.
už periodická není.
A další poznámka, nepíšeme v češtině cosinus, ale kosinus, podobně jako kotangens. Kromě periodičnosti to pak zavání i chybou :-)
Offline
#85 25. 08. 2008 08:24
Re: Limity
↑ Pavel:
Dirichletova funkce je periodická např. s periodou p=1. Ale nejsem si jistý, jestli jsem někdy takový příklad periodické funkce viděl uvedený. Zajímalo by mě celkem, jak je to s minimální periodou funkce. Totiž minimální perioda je taktéž perioda funkce, tedy minimální perioda je kladné číslo, které musí být ale menší než libovolné kladné racionální číslo (nebo? D(x+p/q)=D(x), pro p/q>0), což je jistě spor. Tedy tak, jak se chápe pojem periodická funkce a minimální perioda, je Dirichletova funkce příkladem funkce, která je periodická (dokonce s libovolnou racionální periodou), avšak neexistuje u ní nejmenší perioda.
Offline
#86 27. 08. 2008 12:39
Re: Limity
Marian a Pavel:
To laicky chápem, no nie celkom vždy to platí, že ak je vo funkcii sinus, kosinus... tak je periodická. Existuje na to, ako to overi? nejaký postup bez toho, aby som si musel kresli? graf?
You know who
(or maybe not)
Offline
#87 27. 08. 2008 13:34 — Editoval BrozekP (27. 08. 2008 13:44)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
↑ matoxy:
Pokud máš periodickou funkci f s periodou p a ne nutně periodickou funkci g ( ), pak funkce
), pak funkce  je také periodická s periodou p.
je také periodická s periodou p.
Nebo ještě líp, pokud budeš mít n periodických funkcí  s periodami
s periodami  a bude platit
a bude platit
a funkci g n proměnných ( ), pak funkce
), pak funkce
bude periodická. Myslím, že tohle většinou stačí na to, abychom mohli o funkci říct, že je periodická.
Doufám, že je to správně, pokud ne, opravte mne, prosím. (Odnikud to nemám, pokusil jsem se pouze o sepsání zřejmého pravidla).
EDIT: Ještě myslím, že by se mohlo hodit: Pokud je funkce f periodická s periodou p, pak funkce  je periodická s periodou
je periodická s periodou  .
.
↑ Marian:
Existuje i jednodušší funkce, která nebude mít minimální periodu - konstantní funkce.
Offline
#88 28. 08. 2008 12:54 — Editoval matoxy (28. 08. 2008 12:59)
Re: Limity
BrozekP: čo znamená táto značka 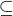 ? A táto
? A táto  ?
?
+ nejak mi nevychádza tento príklad: Vyšetrite priebeh funkcie:  .
.
- usúdil som, že ide o 3-itú zloženú funkciu. Tak som ju zderivoval:
Ak chcem nájs? lokálne extrémy, tak položím túto deriváciu rovnú nule, čím dostanem: 
Jeden z koreňov tejto rovnice je 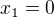 a druhý
a druhý  . Určil som si intervali
. Určil som si intervali 
Tu (príklad 62.) však uvádzajú úplne iný výsledok.
Mohly by ste sa na to niekto pozrei?, kde tam mám chybu?
You know who
(or maybe not)
Offline
#89 28. 08. 2008 13:43 — Editoval BrozekP (28. 08. 2008 14:01)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
↑ matoxy: znamená, že A je podmnožina B nebo je rovna množině B (analogicky k
znamená, že A je podmnožina B nebo je rovna množině B (analogicky k 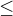 pro čísla). Často se to píše jenom jako
pro čísla). Často se to píše jenom jako  a přesto se tím připouští i rovnost.
a přesto se tím připouští i rovnost.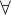 je značka "pro všechna".
je značka "pro všechna".  - tím jsem jenom napsal, že všechny periody jsou vzájemně v poměru racionálních čísel. Pokud si vezmeme funkci
- tím jsem jenom napsal, že všechny periody jsou vzájemně v poměru racionálních čísel. Pokud si vezmeme funkci  , tak ta například není periodická. Funkce
, tak ta například není periodická. Funkce  je periodická s periodou 70.
je periodická s periodou 70.
K průběhu funkce:
Obor hodnot je zřejmě [0,1], takže minima nabývá funkce tam, kde
Podobně s maximy:
Takže jim tam chybí odmocnina u  . Dalo by se to řešit i přes derivace, ale tam si musíš dávat pozor na kraje intervalů, na kterých je funkce definována. Také ne všechny body, kde vyjde derivace nulová, jsou v definičním oboru funkce. Tak jak jsem to řešil je to mnohem jednodušší.
. Dalo by se to řešit i přes derivace, ale tam si musíš dávat pozor na kraje intervalů, na kterých je funkce definována. Také ne všechny body, kde vyjde derivace nulová, jsou v definičním oboru funkce. Tak jak jsem to řešil je to mnohem jednodušší.
Offline
#90 28. 08. 2008 14:03 — Editoval ttopi (28. 08. 2008 14:04)
Re: Limity
BrozekP napsal(a):
↑ matoxy:
znamená, že A je podmnožina B nebo je rovna množině B (analogicky k
pro čísla). Často se to píše jenom jako
a přesto se tím připouští i rovnost.
To by mohlo souviset s tím, že každá množina je sama sobě podmnožinou - tím pádem se rovnost nemusí připouštět, stačí pouze, že je podmnožinou, tedy 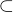
oo^0 = 1
Offline
#91 28. 08. 2008 14:27 — Editoval BrozekP (28. 08. 2008 14:34)
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
↑ ttopi:
Pokud právě bereme symbol  ve smyslu
ve smyslu  , pak neplatí
, pak neplatí  . Toto značení odpovídá novějšímu značení podle normy "ČSN ISO 31-11 Matematické znaky a značky používané ve fyzikálních vědách a technice" přijaté v roce 1998 (Vycházím z Matematické, fyzikální a chemické tabulky & vzorce pro střední školy, Jiří Mikulčák, 2003, nakladatelství Prometheus. Přístup přímo k normě nemám.)
. Toto značení odpovídá novějšímu značení podle normy "ČSN ISO 31-11 Matematické znaky a značky používané ve fyzikálních vědách a technice" přijaté v roce 1998 (Vycházím z Matematické, fyzikální a chemické tabulky & vzorce pro střední školy, Jiří Mikulčák, 2003, nakladatelství Prometheus. Přístup přímo k normě nemám.)
Tím ovšem nechci nikoho nutit se řídit přesně podle norem :-). To bychom museli například používat: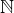 pro přirozená čísla včetně nuly
pro přirozená čísla včetně nuly pro přirozená čísla bez nuly
pro přirozená čísla bez nuly , nikoliv
, nikoliv 
 pro dekadický logaritmus x
pro dekadický logaritmus x
Offline
#92 28. 08. 2008 14:34
Re: Limity
↑ BrozekP:
Já jsem přece rovnost nevyloučil. Jen jsem považoval za zbytečné to zvýrazňovat tou čárkou, když i totožná množina je podmnožinou, proto volím jednoduše 
oo^0 = 1
Offline
#93 28. 08. 2008 14:41
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
↑ ttopi:
Podle té normy ale každá množina je svou podmnožinou pouze ve smyslu  nikoli ve smyslu
nikoli ve smyslu  . Je to zcela analogické značení
. Je to zcela analogické značení  pro čísla. To, že se běžně tato norma ingnoruje, je věc jiná.
pro čísla. To, že se běžně tato norma ingnoruje, je věc jiná.
Offline
#94 28. 08. 2008 14:45
Re: Limity
BrozekP:
- k tej funkcii. Ako prídem k tomu, čo je obor hodnôt funkcie? Možno sa to už učilo kedysi v deviatej triede, ale akosi si neveim spomenú? ako sa to robí.
- k tej periodičnosti. Ako ste prišli k tomu, že tieto funkcie:  ,
,  sú či niesú periodické?
sú či niesú periodické?
You know who
(or maybe not)
Offline
#95 28. 08. 2008 15:07
- Pavel Brožek


- Místo: Praha
- Příspěvky: 5694
- Škola: Informatika na MFF UK
- Pozice: Student
- Reputace: 194
Re: Limity
Obor hodnot je většinou zřejmý, když si funkci projdeš od té nejvnitřnější, ukážu na příkladu  . Obor hodnot funkce
. Obor hodnot funkce  je
je  . Obor hodnot
. Obor hodnot  je proto [-1,1]. Zřejmě ale musí být pod odmocninou nezáporné číslo, takže taková x, pro která je
je proto [-1,1]. Zřejmě ale musí být pod odmocninou nezáporné číslo, takže taková x, pro která je  záporný nejsou v definičním oboru f.
záporný nejsou v definičním oboru f.  má tedy pro x z definičního oboru f obor hodnot [0,1]. A odmocnina zobrazí interval [0,1] opět na interval [0,1].
má tedy pro x z definičního oboru f obor hodnot [0,1]. A odmocnina zobrazí interval [0,1] opět na interval [0,1].
Není na tom nic tak složitého, ani si nevzpomínám, že by se to někdy učilo. Je třeba se jen trochu zamyslet nad funkcemi z kterých se výsledná funkce skládá. Někdy je potřeba spočítat nějakou tu derivaci, abychom určili maxima a minima. Nevím jestli na určení oboru hodnot existuje nějaký standardní postup.
K té periodicitě:
Proto je periodická. Jak jsem přišel na to, že je to číslo 70? Jde o nejmenší společný násobek period těch dvou sinů. není periodická. Nenapadá mě jak bych to jednoduše ukázal, trochu to je vidět z toho, že periody, které jsou v poměru iracionálního čísla "nemají nejmenší společný násobek".
není periodická. Nenapadá mě jak bych to jednoduše ukázal, trochu to je vidět z toho, že periody, které jsou v poměru iracionálního čísla "nemají nejmenší společný násobek".
Offline
#96 29. 08. 2008 18:57 — Editoval matoxy (29. 08. 2008 18:58)
Re: Limity
BrozekP ten definičný obor už chápem. Len som myslel, že som zabudol na nejaký spôsob ako sa to robilo.
Tá periodicita, tam mi robí hlavne problém moja, ako som cez prázdniny zistil, dos? slabá znalos? goniometire. No časom to hádam pochopím lepšie.
You know who
(or maybe not)
Offline
#97 01. 09. 2008 09:04
Re: Limity
Koniec prázdnin je tu už naozaj dnes a zajtra sa treba pobra? do školy. Celkom rýchlo ubehlo tých 66 dní. Cez prázdniny som sa však okrem čerpania nových síl a nápadov do ďalšieho školského roku trochu povenoval aj matematike, pričom mi pomohlo aj pár ľudí z tohto fóra. Zvláš? ďakujem Jelene, ktorá mi dos? pomohla nie len v tejto téme, samozrejme však aj všetkým ostatným, ktorý mi venovali kus času.
You know who
(or maybe not)
Offline
