Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#6 26. 12. 2011 19:39 — Editoval Oxyd (26. 12. 2011 19:41)
Re: Integrál, derivace
 je přece konstanta.
je přece konstanta.
Navíc tady bych asi per partes nepoužíval. Hezky bych to rozdělil na rozdíl dvou integrálů, konstanty vyhodil před integrály a pak na každý z nich použil jednoduchou substituci.
Mýlím se častěji, než bych chtěl. Pokud vám v mém příspěvku něco nehraje, neváhejte se zeptat.
Jsem stále mlád a je mi příjemnější tykání. :)
Offline
#12 26. 12. 2011 21:18
Re: Integrál, derivace
Tak to už nevím, pokud to ale jde, nejpíš to nebude lehčí než s substitucí, ať se k tomu případně vyjádří někdo další :). Pokud bys chtěl se naučit substituci napřed, tak si projdi třeba tohle.
Jinak ale ten cos(8x), co jsi počítal v příkladu předtím, jsi počítal jak? To je totiž taky ze substituce.
Offline
#14 27. 12. 2011 09:12
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál, derivace
Zdravím vás,
jen na doplnění - je možné, že této metodě se neříká "substituce" (osobně tomu říkám "malá substituce", na Východě se tomu říka "uvedení pod znak diferenciálu"). Potom jsem viděla, že takové "malé substituce" jsou považovany za "tabulkové vzorce" (tuším, v učebnici MZLU pro ekonomy bylo) např. 
Je potřeba prokonzultovat některou ze zde uvedených úloh? (nějak se neumím zorientovat :-) Případně použijte online nástroje úvodního tématu sekce VŠ (doporučuji MAW). Ať se vede.
Offline
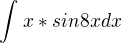


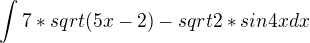

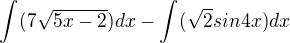
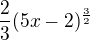 ?
?