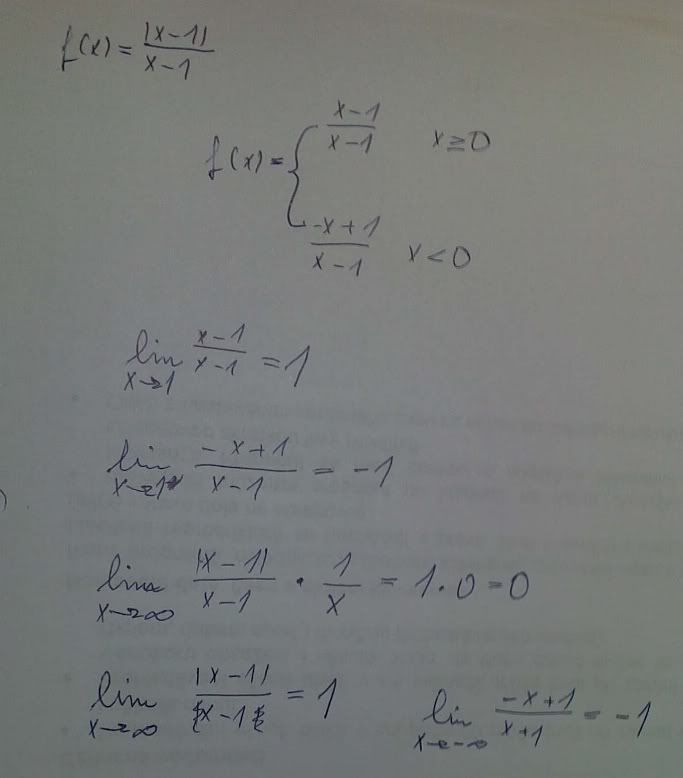Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 26. 12. 2011 23:39
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Asymptoty funkce
Zdravím,
takové drobnosti - odstranění absolutní hodnoty v čitateli se provádí pro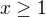 
a pro 
(ne 0, jak máš napsáno, zřejmě překlep nebo nepozornost).
Vyšetření asymptot bez směrnice (v pořádku), hodilo by se upřesnit, že vyšetřujeme zprava (pro x k 1+ pro první odstranění abs. hodnoty a pro x k 1- pro druhé odstranění abs. hodnoty). A z definice asymptoty bez směrnice bylo prokázáno, že takové nejsou (není to na scanu uvedeno).
Asymptoty se směrnici - viz definice - třeba "doplnit" až do zápisu pro rovnici asymptoty (přímky) 
(a je 0 jak pro +oo, tak pro -oo), b je dopočteno (1 a -1), ale rovnice asymptoty se směrnici sestavena ještě není.
Snad jsem nic nepřehlédla.
Offline