Matematické Fórum

Linda · 06. 06. 2008 15:55

Ahojky, potrebuju moc poradit s timhle prikladem. Dekuju :-)
Uvazujeme trojuhelnik v rovine A=[4,2] , B=[5,5],C=[1,3] vzpocitejte polomer opsany kruznice.

O.o · 06. 06. 2008 16:05 — Editoval O.o (06. 06. 2008 16:06)

↑ Linda:
Já bych si to nejprve nakreslil, pak pokud je to na wikiepdii správně, tak (podle wiki) platí vztah r=a/sin(alfa). Když znáš všechny strany, tak není problém spočítat úhel alfa a dosadit do té rovnice stanu a a daný úhel.
Jinak by to asi také šlo, že si vypočteš středy stran trojúhelníku, pak si napíšeš aobecnou rovnici přímek, které protínají střed trojúhelníku a zároveň střed strany (těžnice?) a z nich vypočítáš souřadnice středu (průsečík těžnic). Poté stačí vypočítat vzdálenost středu trojúhelníku od jednoho z vrcholů (bodů) trojúhelníku.

Olin · 06. 06. 2008 16:10

Tak to mě napadá asi tisíc způsobů, jak to řešit… Např. že si určíš velikost jedné strany, úhel proti ní a pak pomocí sinové věty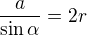
$\frac{a}{\sin \alpha} = 2r$

Jiný způsob je nalézt rovnice os dvou stran, jejich řešením dostaneme souřadnice středu kružnice opsané a pak už jen zjistíme vzdálenost od libovolného z vrcholů.

A způsob, který se mi líbí asi nejvíc, je přes vzdálenosti od bodů. Musí totiž platit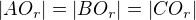
$|AO_r| = |BO_r| = |CO_r|$
tedy
$(x - 4)^2 + (y - 2)^2 = r^2\nl (x - 5)^2 + (x - 5)^2 = r^2\nl (x - 1)^2 + (y - 3)^2 = r^2$
V této soustavě se snadno zbavíme členů s druhou mocninou a dál už je to jednoduché.

apurvathea · 02. 09. 2008 19:26

prosim, jak zjistim velikost strany a uhlu?

Pavel Brožek · 02. 09. 2008 20:15

↑ O.o:

Průsečík těžnic $\neq$ střed kružnice opsané.

↑ apurvathea:

Velikost strany zjistíš jednoduše jako vzdálenost dvou vrcholů. Velikost úhlu asi pomocí kosinové věty.

apurvathea · 02. 09. 2008 20:53

jo to je mi jasne, ze to je vzdalenost dvou vrcholu. Ale kdyz jsou body urceny jako tady v zadani, jak se z toho vypocita velikost strany.?

Pavel Brožek · 02. 09. 2008 21:11

↑ apurvathea:

Ty body v zadání jsou vrcholy trojúhelníku. Pro vzdálenost dvou bodů platí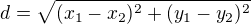

$d=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

Velikost strany a je vzdálenost vrcholů B a C. Nevím co k tomu víc říct.

Cheop · 03. 09. 2008 08:25 — Editoval Cheop (03. 09. 2008 09:02)

Řešení - viz obrázek

http://forum.matweb.cz/upload/642-troj.jpg

Délky stran trojúhelníku jdou pochopitelně určit ze vztahu, který Ti nastínil BrozekP.

Oprava:
Protože je trojúhelník pravoúhlý (pravý úhel při vrcholu A) pak poloměr předmětné kružnice musí být opravdu 1/2 strany BC (a).
Takže, abychom zjistili úhel $\alpha$ musíme pro výpočet použít kosinovou větu.

Matematické Fórum

#1 06. 06. 2008 15:55

trojuhelnik v rovine

#2 06. 06. 2008 16:05 — Editoval O.o (06. 06. 2008 16:06)

Re: trojuhelnik v rovine

#3 06. 06. 2008 16:10

Re: trojuhelnik v rovine

#4 02. 09. 2008 19:26

Re: trojuhelnik v rovine

#5 02. 09. 2008 20:15

Re: trojuhelnik v rovine

#6 02. 09. 2008 20:53

Re: trojuhelnik v rovine

#7 02. 09. 2008 21:11

Re: trojuhelnik v rovine

#8 03. 09. 2008 08:25 — Editoval Cheop (03. 09. 2008 09:02)

Re: trojuhelnik v rovine

Zápatí